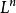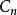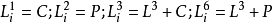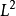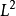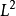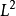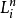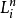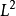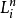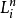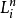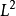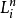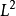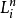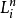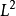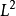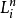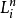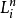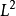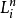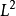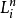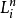點群定義
在固體物理中,點群與
晶類(crystal class)有等同的含義。
對稱操作群:由物體的對稱操作構成的群。
對稱操作:物體在
正交變換(保持兩點間距離不變的幾何操作,如旋轉,反伸,反映)下不變,則該變換為物體的對稱操作。
群:
數學概念,集合和其上的一種運算構成一個群。群要求滿足封閉性,存在單位元素,存在
逆元素,滿足該運算的
結合律;簡單說群是按照某種規律相互聯繫著的一組元素的集合。群的元素可以是字母、數字等,在晶體對稱理論中,群的元素是
對稱操作。
對稱要素
對稱要素包括
對稱中心、
對稱軸、
對稱面、
旋轉反伸軸和
旋轉反映軸。對稱要素可用普通符號、國際符號和Schoenflies 符號三種方式表示。可以證明,晶體中對稱要素共有8種。分別是1,2,3,4,6 ,m,i,-4(這裡用國際符號表示,
準晶中還可以出現其他對稱要素)。
對稱軸:對稱軸是一根假象直線,n重
旋轉軸是指若物體繞某軸轉2π/n 及2π/n的整數倍,物體不變,則該軸為物體的n重旋轉軸。
對稱面:對稱面是一個假象的平面,相應的
對稱操作為對於此平面的反映。它將圖形平分為互為鏡像的兩個相等部分。
對稱中心:對稱中心是一個假象的點,相應的
對稱操作是對此點的反伸(或稱倒反)。如果通過此點作任意直線,則在此直線上距對稱中心等距離的兩端,必定可以找到對應點。
旋轉反伸軸:旋轉反伸軸是一根假象直線,若物體對某軸作轉2π/n 加上中心反伸的聯合操作,及聯合操作的倍數,物體不變,則該軸為物體的n重旋轉反伸軸。
其中,除了
外,其餘各種
旋轉反伸軸都可以用其它簡單的
對稱要素或它們的組合來代替,期間關係如下:
旋轉反映軸:旋轉反映軸是一根假象直線,若物體對某軸作轉2π/n 加上對垂直它的一個平面進行反映的聯合操作,及聯合操作的倍數,物體不變,則該軸為物體的n重
旋轉反伸軸。
對稱要素的組合
在結晶多面體中,可以有一個
對稱要素單獨存在,也可以有若干個對稱要素組合在一起共存。
對稱要素組合服從如下規律:
1)如果有一個二次軸
垂直n次軸
,則必有n個
垂直與
,即
x
→
n
。
2)如果有一個
對稱面P垂直偶次軸
(n為偶數),則在其交點存在
對稱中心C,即
xP→
PC。
3)如果有一個
對稱面P包含
對稱軸,則必有n個P包含
,即
xP→
nP。
4)如果有一個二次軸垂直與
旋轉反伸軸,或者有一個
對稱面P包含
,當n為奇數時必有n
垂直
和n個對稱面包含
,即
x
→
n
nP,
xP→
n
nP;當n為偶數時必有n/2個
垂直
和n/2個P包含
,即
x
→
n/2
n/2P,
xP→
n/2
n/2P。
點群介紹
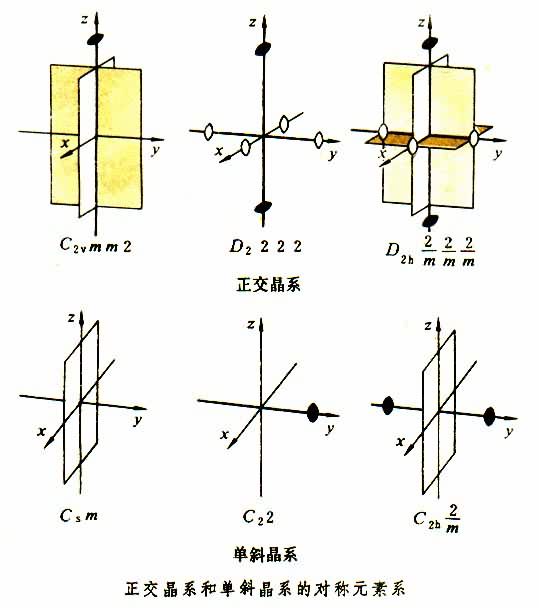
對稱性是晶體的一個共性,結晶多面體中,全部
對稱要素的組合,稱為該結晶多面體的點群(也稱對成型)。
14種Bravais(布拉維)格子:簡單三斜、簡單單斜、底心單斜、簡單正交、底心正交、體心正交、面心正交、三角、簡單四方、體心四方、六角、簡單立方、體心立方、面心立方;
32個
晶類(點群):C
1、C
i、C
2、C
s、C2h、D
2、D
2v、D
2h、C
3、C
3i、D
3、C
3v、D
3d、C
4、C
4h、D
4、C
4v、D
4h、S
4、D
2d、C
6、C
6h、D
6、C
3v、D
6h、C
3h、D
2h、T、T
h、T
d、O、O
h(這裡用 Schoenflies 符號表示,還可以用國際符號表示,請參考相關書目) 。
沿著立方軸轉π/2,π,3π/2,有3個立方軸,共9種
沿著
體對角線轉2π/3,4π/3,有4條體對角線,共8種
不動算1種,共9+6+8+1=24種。
這24種轉動加上中心
反演也有24種,故共48種,記為Oh,其中24種純轉動記為O。

有了點群的劃分,我們就可以表示任何一種晶體具體的結構
對稱性。點群的國際符號一般由三位組成,分別表示三個特定方向上的
對稱元素,不同
晶系中三個方向的選取自然不同。如
鈦酸鋇的六方晶系就可表示為6/mmm 。由於很多內容在這裡因沒有相應的編輯器,敘述不便,更多的內容也看可以參考書目。
準晶點群
1984年在AlMn合金的
透射電子顯微鏡的研究中首次發現了五次
對稱軸;其顆粒的點群為m-3-5.在其結構中
配位多面體是
長程有序的,但沒有平移周期,即不具有格子構造。這類物質陸續發現,它們被認為是介於
非晶態和結晶態之間的一中新物態——準晶態。
在五次軸的
準晶之後,繼而又有十次軸準晶的研究。從而推導出的新點群如下:
五方晶系:5 ;-5 ;5m ;-5m ;52
十方晶系:10 ;-10 ;10m ;-10m ;10,2 ;10/m ;10/mmm