基本介紹
- 中文名:晶體學點群
- 提出者:約翰·弗里德里希·克里斯蒂安·赫塞爾
- 提出時間:1830
- 套用學科:晶體學
釋義
 晶體學點群
晶體學點群 晶體學點群
晶體學點群實驗
 晶體學點群
晶體學點群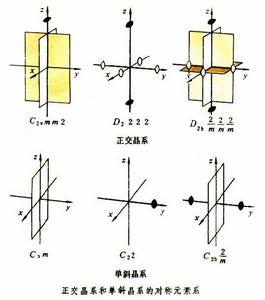 晶體學點群
晶體學點群 晶體學點群
晶體學點群 晶體學點群
晶體學點群記號
熊夫利記號
- 更多資料:三維點群
- S2n(源自德語Spiegel,意思是鏡面)表示一根只含有2n次旋轉反映軸(簡稱映軸)。
- Dn(二面體群)表示這個群只有一根n次旋轉軸和n根垂直於這根主軸的二重軸。Dnh是加上一個與n次旋轉軸垂直的鏡面。Dnd則是Dn是加上n個與n次旋轉軸平行的鏡面。
- 字母T(四面體)表示這個群有四面體的對稱性。Td則包括了旋轉反映操作,T群本身則不包含旋轉反映操作,Th則是T群加上與旋轉軸垂直的鏡面。
| n | 1 | 2 | 3 | 4 | 6 |
|---|---|---|---|---|---|
Cn | C1 | C2 | C3 | C4 | C6 |
Cnv | C1v=C1h | C2v | C3v | C4v | C6v |
Cnh | C1h | C2h | C3h | C4h | C6h |
Dn | D1=C2 | D2 | D3 | D4 | D6 |
Dnh | D1h=C2v | D2h | D3h | D4h | D6h |
Dnd | D1d=C2h | D2d | D3d | D4d | D6d |
S2n | S2 | S4 | S6 | S8 | S12 |
赫爾曼–莫甘記號
1 | 1 | |||||
2 | ⁄m | 222 | m | mm2 | mmm | |
3 | 3 | 32 | 3m | 3m | ||
4 | 4 | ⁄m | 422 | 4mm | 42m | ⁄mmm |
6 | 6 | ⁄m | 622 | 6mm | 62m | ⁄mmm |
23 | m3 | 432 | 43m | m3m |
對應關係
| 晶族 | 晶系 | 赫爾曼–莫甘 (完整記號) | 赫爾曼–莫甘 (簡寫記號) | 舒勃尼科夫 | 熊夫利 | 軌形記號 | 考克斯特記號 | 順序 |
|---|---|---|---|---|---|---|---|---|
三斜 | 1 | 1 | C1 | 11 | [ ] | 1 | ||
 |  | Ci= S2 | x | [1,2] | 2 | |||
2 | 2 | C2 | 22 | [2] | 2 | |||
m | m | Cs= C1h | * | [ ] | 2 | |||
2/m | C2h | 2* | [2,2] | 4 | ||||
222 | 222 | D2= V | 222 | [2,2] | 4 | |||
mm2 | mm2 | C2v | *22 | [2] | 4 | |||
mmm | D2h | *222 | [2,2] | 8 | ||||
4 | 4 | C4 | 44 | [4] | 4 | |||
 |  | S4 | 2x | [2,4] | 4 | |||
4/m | C4h | 4* | [2,4] | 8 | ||||
422 | 422 | D4 | 422 | [4,2] | 8 | |||
4mm | 4mm | C4v | *44 | [4] | 8 | |||
 |  | D2d | 2*2 | [2,4] | 8 | |||
4/mmm | D4h | *422 | [4,2] | 16 | ||||
3 | 3 | C3 | 33 | [3] | 3 | |||
 |  | S6= C3i | 3x | [2,6] | 6 | |||
32 | 32 | D3 | 322 | [3,2] | 6 | |||
3m | 3m | C3v | *33 | [3] | 6 | |||
 |  | D3d | 2*3 | [2,6] | 12 | |||
6 | 6 | C6 | 66 | [6] | 6 | |||
 |  | C3h | 3* | [2,3] | 6 | |||
6/m | C6h | 6* | [2,6] | 12 | ||||
622 | 622 | D6 | 622 | [6,2] | 12 | |||
6mm | 6mm | C6v | *66 | [6] | 12 | |||
 |  | D3h | *322 | [3,2] | 12 | |||
6/mmm | D6h | *622 | [6,2] | 24 | ||||
23 | 23 | T | 332 | [3,3] | 12 | |||
3 | m3 | Th | 3*2 | [3,4] | 24 | |||
432 | 432 | O | 432 | [4,3] | 24 | |||
 |  | Td | *332 | [3,3] | 24 | |||
3 | m3m | Oh | *432 | [4,3] | 48 | |||
