基本介紹
- 中文名:面積積分
- 又稱:面積函式
- 提出者:Η.Η.盧津
- 涉及學科:數學
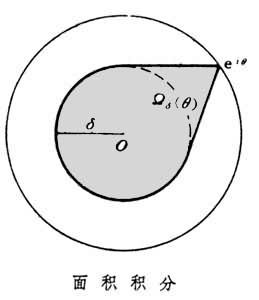
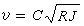
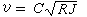
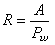

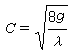



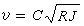
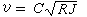
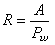


又稱面積函式,是蘇聯數學家。Η.Η.盧津1930年首先引入的一種特殊積分。...... 又稱面積函式,是蘇聯數學家。Η.Η.盧津1930年首先引入的一種特殊積分。...
積分是微積分學與數學分析里的一個核心概念。通常分為定積分和不定積分兩種。直觀地說,對於一個給定的正實值函式,在一個實數區間上的定積分可以理解為在坐標平面...
定積分是積分的一種,是函式f(x)在區間[a,b]上積分和的極限。這裡應注意定積分與不定積分之間的關係:若定積分存在,則它是一個具體的數值(曲邊梯形的面積),...
盧津面積積分(Lusin area integration)是刻畫函式在Lp中大小的一種運算元。...... 盧津面積積分(Lusin area integration)是刻畫函式在Lp中大小的一種運算元。...
面積分又稱“曲面積分”,是將積分域由平面塊推廣到曲面塊的重積分。...... 面積分又稱“曲面積分”,是將積分域由平面塊推廣到曲面塊的重積分。中文名 面積分 ...
極坐標定積分是以R為半徑,θ為積分變元,計算曲線周長的、面積的積分。曲線的周長定積分為,曲線的面積定積分為。設曲線ρ=R在區間[θ1,θ2]上非負連續,當d...
物體所占的平面圖形的大小,叫做它們的面積。面積就是所占平面圖形的大小,平方米,平方分米,平方厘米,是公認的面積單位,用字母可以表示為(m²,dm²,cm²)。...
勒貝格積分,是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的函式的積分可以看作是求其函式圖像與軸之間的面積。...
二重積分是二元函式在空間上的積分,同定積分類似,是某種特定形式的和的極限。本質是求曲頂柱體體積。重積分有著廣泛的套用,可以用來計算曲面的面積,平面薄片重心等...
面積公式,其中包括長方形面積公式、正方形面積公式、扇形面積公式,圓形面積公式,弓形面積公式,菱形面積公式,三角形面積公式,梯形面積公式等多種圖形的面積公式。...
定義在曲面上的函式或向量值函式關於該曲面的積分。曲面積分一般分成第一型曲面積分和第二型曲面積分。第一型曲面積分物理意義來源於對給定密度函式的空間曲面,計算...
定義在曲面上的函式關於該曲面的積分。第一型曲線積分物理意義來源於對給定密度函式的空間曲面,計算該曲面的質量。...
積分檢驗法是汽液平衡數據熱力學一致性檢驗的一種較常用的方法,由於實驗測定汽液平衡數據時往往控制在等溫或等壓條件下,故汽液平衡數據的一致性檢驗也分為等溫和...
如果函式f(x,y)在有界閉區域D上連續,區域D的面積為S,且 m 和 M 分別是f(x,y)在D上的最小值和最大值,則mS ≤∫∫f(x,y)在D上的二重積分 ≤ MS...
黎曼積分(Riemann Integral),也就是所說的正常積分、定積分。在實分析中,由黎曼創立的黎曼積分首次對函式在給定區間上的積分給出了一個精確定義。黎曼積分在技術上...
若球半徑是R,球冠的高是h,球冠面積是S,則S=2πRh,若球冠的底的半徑是r,則S=π(r^2+h^2)。...
橢圓面積公式:S=π(圓周率)×a×b,其中a、b分別是橢圓的半長軸,半短軸的長。橢圓面積公式屬於幾何數學領域。...
截面(英語:Cross section)為一幾何學名詞,是指一三維空間下的物體和一平面相交所產生交集。截面的面積稱為截面積。...
曲線下面積area under the cure;AUC給藥後以血藥濃度為縱坐標,以時間為橫坐標所得曲線下的面積。...
勒貝格積分(英語:Lebesgue integral)是現代數學中的一個積分概念,它將積分運算擴展到任何測度空間中。在最簡單的情況下,對一個非負值的函式的積分可以看作是函式...
曲面面積(area of a surface)是指曲面表面的面積。把光滑曲面S分成沒有公共內點的n塊S1,... , Sn,且每一塊仍是光滑曲面,在每個S上取一點P,過P作S的切...
