橢圓面積公式:S=π(圓周率)×a×b,其中a、b分別是橢圓的長半軸,短半軸的長。橢圓面積公式屬於幾何數學領域。
基本介紹
- 中文名:橢圓面積公式
- 表達式:S=π×a×b
- 套用學科:數學
- 適用領域範圍:幾何數學領域
面積公式
定理內容
導數方法
陰影面積
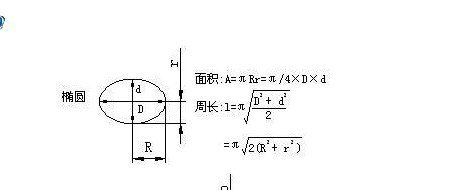

橢圓面積公式:S=π(圓周率)×a×b,其中a、b分別是橢圓的長半軸,短半軸的長。橢圓面積公式屬於幾何數學領域。


橢圓面積公式:S=π(圓周率)×a×b,其中a、b分別是橢圓的長半軸,短半軸的長。橢圓面積公式屬於幾何數學領域。...
面積公式,其中包括長方形面積公式、正方形面積公式、扇形面積公式,圓形面積公式,弓形面積公式,菱形面積公式,三角形面積公式,梯形面積公式等多種圖形的面積公式。...
橢圓面積公式 (其中 分別是橢圓的長半軸、短半軸的長),或 (其中 分別是橢圓的長軸,短軸的長)。證: 的面積,由於圖形的對稱性可知,只要求出第一象限的面積...
分別是橢圓的長半軸、短半軸的長,可由圓的面積可推導出來)或 (其中 分別是...3. 左華榮.高中數學公式定理理解與套用手冊:[M].成都:四川出版集團·四川辭書出版...
橢圓面積計算公式橢圓面積公式: S=πab橢圓面積定理:橢圓的面積等於圓周率(π)乘該橢圓長半軸長(a)與短半軸長(b)的乘積。以上橢圓周長、面積公式中雖然沒有...
(4)面積= (∠F1PF2=θ)橢圓焦點三角形證明 編輯 橢圓焦點三角形運用公式 設P為橢圓上的任意一點P(不與焦點共線),∠F2F1P=α ,∠F1F2P=β,∠F1PF2=...
概述是一種幾何形狀。類似於橢圓。周長計算沒有公式,但有積分形式的表達: 最早由伯努利(那個不記得了)提出,歐拉發展 對這類問題的討論引出一門數學分支--橢圓積分...
圓面積公式是一種定理定律。為圓周率*半徑的平方,用字母可以表示為:S=πr²或S=π*(d/2)²。(π表示圓周率(3.1415926……),r表示半徑,d表示直徑)。...
球體(正球)表面積: {球體(正球)表面積=圓周率×半徑×半徑×4}橢圓 (其中π(圓周率,a,b分別是橢圓的長半軸,短半軸的長).半圓: (半圓形的面積公式=圓周率...
2)面積公式:S=πab 橢圓面積定理:橢圓的面積等於圓周率(π)乘該橢圓長半軸長(a)與短半軸長(b)的乘積。 3、扇形面積: 圓心角為n°,半徑為r的扇形面積為(...
1 面積的由來 2 面積的單位 3 面積計算公式 圖形面積面積的由來 編輯 面積...橢圓:詞條圖冊 更多圖冊 參考資料 1. 李懷源.哇!好有趣的數學 師軒版 3:...
橢圓旋轉(revolution of an ellipse)是一種平面仿射變換,即將橢圓繞其中心旋轉的平面仿射變換。在平面直角坐標系中,橢圓旋轉τ:(x,y)→(x′,y′)的計算公式為...
對常用幾何形體進行周長、面積、體積計算,包括、矩形、三角形、平行四邊形、梯形、圓球、圓柱、圓錐、圓錐台、球冠與球缺、橢圓、橢球、正多邊形、環形、扇形、弓形...
