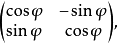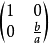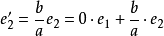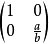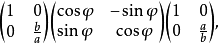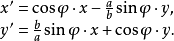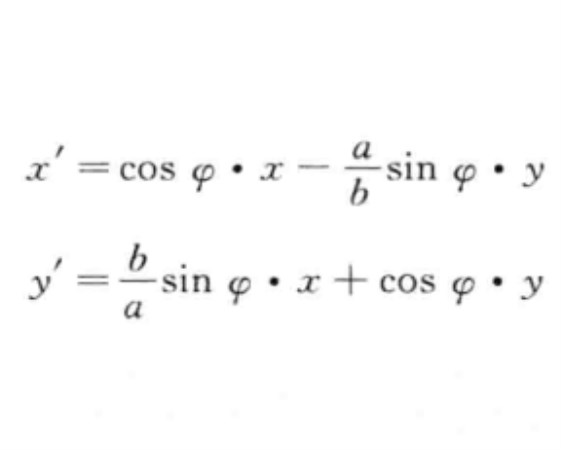基本介紹
平面上把橢圓變成自己的仿射變換用平面上把圓周變成自己的仿射變換來誘發
下面討論的是平面上把橢圓變成自己的
仿射變換,也就是把已知橢圓的每個點變成這個橢圓的點的仿射變換,這樣的變換是存在的,要說明它們,比較直觀的是把橢圓看作圓周的正射影。
設E是橢圓S的平面,E是圓周
的平面,圓周
是投射成橢圓S的,平面E的每個變換自動產生——或者說是“誘發”——平面
的變換,那就是說,在這個變換下,平面
的每個點
,投射到平面E的點A的,變成平面
的點
,它投射到點A的象B。同樣,平面
的每個變換誘發出平面E的變換,這時很顯然,如果這些變換的一個是仿射的,則另一個也是仿射的,因為在射影下共線的三個點還變成共線的三個點。同樣顯然,如果平面E的變換把橢圓S變成自己,則它所誘發的平面
的變換把圓周
變成自己,反之亦然。這樣一來,在平面上發掘把橢圓變成自己的仿射變換的問題,就歸於在平面上發掘把圓周變成自己的仿射變換的問題。
橢圓旋轉 平面
繞著它上面的一個圓周的中心的旋轉,顯然是把這個圓周變成自己的平面
的
仿射變換。它所誘發的平面E的變換叫作
橢圓旋轉。因此,橢圓旋轉是那樣的變換,在一個平面實行繞著一個固定點的普通的旋轉時,平面的點的射影就作著由這個變換所造成的變化,簡短地說來:橢圓旋轉是普通旋轉的射影。
因為普通的旋轉是等仿射變換,也就是不改變面積的仿射變換,而且在射影下面積的相等性保留不變,所以橢圓旋轉也是等仿射變換。
在平面
的(普通的)旋轉下,如果構想有著一種連續旋轉的過程,使得這個平面的點向著同一個方向畫出同中心的圓弧,它們從旋轉中心看來是轉了同一個角度的。這些圓周投射到平面E中成為同中心的橢圓,並且由於上面的圓周是同位相似的。這些橢圓也同位相似。因此,在橢圓旋轉下。平面的所有點向著同一個方向畫出同中心的同位相似的橢圓弧,並且同一個橢圓的半徑掃過同樣面積的橢圓扇形。
當我們從遠處側面觀看轉動著的輪子時,我們就看到近似的橢圓旋轉(圖1)。如果我們是從無窮遠處來做觀察的,則輪子的運動就正確地表達出橢圓旋轉來。
 圖1
圖1橢圓旋轉的角
平面上繞著固定點的旋轉可以由一個已知數目完全決定,那就是旋轉角,這時常把反時針方向的旋轉算是正的,順時針方向的旋轉算是負的.旋轉角測量的方便在於它的數值是可加的,這是指在繼續實行旋轉時它的角可以加起來這一點而說的。這種可加的數值對於橢圓旋轉也可以引出,只要簡單地轉移到誘發橢圓旋轉的普通的旋轉,這時自然保留著角這個名稱。這樣一來,按定義說,橢圓旋轉的角是指誘發橢圓旋轉的普通旋轉的角。
橢圓旋轉的角可以用更直接的方法定義,並且是用純仿射的術語說的,這就是在確立了普通旋轉角的定義以後,直接把這個定義推廣到任意的橢圓旋轉.用弧度表示普通的旋轉角,通常是定義為任意點所畫的弧的長度與這條弧的半徑之比值.這個定義不是仿射的,因為不平行的線的長度的比值在仿射變換下一般說來是不能保留的,然而用弧度表示的普通的旋轉角,還是任意點從轉動中心出發的半徑所掃過的扇形面積的兩倍與這個半徑的平方之比值,所謂半徑的平方也就是作在已知點所畫弧的圓周的一對共軛半徑上的平行四邊形(也就是正方形)的面積.角的這樣的定義可以直接推廣到任意的橢圓旋轉.那就是說,橢圓旋轉的角,是任意點從中心出發的半徑所掃過的橢圓扇形面積的兩倍、與作在已知點所畫弧的橢圓的一對共軛半徑上的平行四邊形(例如作在半軸上的長方形)面積之比值.
用S表示任意點的半徑所掃過的面積,用a和b表示這個點所畫弧的橢圓的半軸,對於橢圓旋轉角我們就有下列表示式
把橢圓變成自己的所有仿射變換的決定
現在來決定平面上把橢圓變成自已的所有仿射變換.顯然,平面對於橢圓對稱軸的反射是這種變換的一個.它與橢圓旋轉不同,至少是由於橢圓旋轉是第一種變換,而反射則是第二類變換.我們來證明,每一個第一種的仿射變換,把橢圓變成自己的,是橢圓旋轉,而每一個第二種的仿射變換,把橢圓變成自己的,則是一個橢圓旋轉加上對於橢圓的一條軸線的一個反射。
我們先來證明關於圓周的對應的斷言.在把橢圓——特別說來,把圓周——變成自己的仿射變換下,中心變成中心,而且每一對共軛半徑還變成一對共軛半徑,因為橢圓半徑的共軛性是仿射性質.但是對於圓周說,共軛半徑互相垂直.因此,在把圓周變成自己的仿射變換下,由圓周的互相垂直的半徑組成的標架,還變成這樣的標架.這就說明,把圓周變成自己的仿射變換,是保留圓周中心不變的正交變換.從關於正交變換的第二基本定理的證明看到,這樣的變換或者是繞著這箇中心的旋轉(如果它是第一種的),或者 是旋轉加上對於通過中心的直線的反射(如果變換是第二種的);這時在後一種情形里反射可以對通過中心的任意預先指定的直線實行.然而把橢圓變成自己的第一種仿射變換,顯然由把圓周變成自己的第一種仿射變換(按著已經證明的,它就是旋轉)誘發而成.因而我們的第一個斷言證明了.完全同樣的,把橢圓變成自己的第二種仿射變換,由把圓周變成自己的第二種仿射變換(按著已經證明的,它是旋轉加上反射)誘發而成.如果我們取作產生平面
的反射的直線的,是這樣的一條直線,它的射影包含著橢圓的一條軸線,那么這個反射雖然就誘發平面E對於橢圓的對應軸線的反射;而平面
的旋轉則誘發平面E的橢圓旋轉.因而我們的第二個斷言也證明了。
上面我們看到,在把圓周變成自己的仿射變換下,由它的兩個互相垂直的直徑組成的標架,變成同樣的標架,顯然,反之,把由圓周的兩個互相垂直的半徑所組成的標架變成同樣的標架的每一個仿射變換,都把圓周變成自己.然而這樣的變換誘發把橢圓的一對共軛半徑變成同樣的一對半徑的變換.因此,我們有下面的結果:
把橢圓變成自己的仿射變換,是而且只是這樣的變換,它們把由橢圓的任意一對共軛半徑所組成的標架,變成同樣的標架。
最後還要提出一個很容易證實的斷言:把橢圓變成自己的仿射變換,也把所有與它共中心的同位相似的橢圓變成自己。
變換誘發的普遍方法
在發掘平面上把橢圓變成自己的仿射變換時,我們利用了把一個平面的仿射變換用正射影誘發另一個平面的仿射變換.這個方法只是普遍的變換誘發方法的一個特別用法。
 圖2
圖2如果在兩個平面E和E'(特別說來,它們可以重合)中間確立了一一對應,則一個平面到自身的每個一一變換就產生另一個平面的“誘發出來的”一一變換,這時兩個平面中間點的對應關係並不被違背,因此,如果在平面E上點A變成點B,則在平面E'上對應的點A'變成對應的點B',反之亦然.在圖2上,σ表示平面E和E’中間作為E到E'的映射的一一對應,τ表示平面E的變換,τ'表示平面E'的誘發出來的變換.從圖上看到,要找出點A'在變換τ'不變成的點B',可以先把A'變成A,也就是用變換σ-1來改變A' ,然後套用變換τ把A變成B,最後套用變換σ把B變成B'.因此:
τ'=στσ-1. (2)
顯然,如果變換τ把平面E的一個圖形變成自己,則它所誘發的變換τ’就把平面E'的對應的圖形變成自己,反之亦然.如果平面E和E'中間的對應是仿射的,平面E的變換也是仿射的,則平面E'的誘發出來的變換,作為(三個)仿射映射的乘積,也是仿射的。
在仿射變換的情形下,從誘發出來的變換的定義直接推出,如果e1,e2是平面E上的坐標標架,e'1,e'2是在平面E和E'中間的仿射對應下它在平面E'上的象,則平面E'的誘發出來的變換對於標架e'1,e'2說的表達公式與平面E的原先的仿射變換對於標架e1,e2說的表達公式完全一樣。
橢圓旋轉的公式
作為上一段里所確立的公式(2)的套用,我們來引出橢圓旋轉的公式。
上面我們曾經把平面的橢圓旋轉當作另一個平面的普通旋轉經過射影誘發出來的變換.然而平面的橢圓旋轉也可以認為是同一個平面的普通旋轉經過壓縮誘發出來的變換.那就是說,把半軸為a和b的橢圓變成自己而且由角φ決定的橢圓旋轉。顯然是由橢圓平面繞著它的中心旋轉同樣角度φ的普通旋轉,經過這個平面向著橢圓的長軸作係數為b/a的壓縮所誘發出來的。
設e1,e2是直角坐標系統的標架,它的軸線順著所討論的橢圓的軸線行進(並且e1順著長軸,e2順著短軸).我們知道,繞著標架的原點旋轉角φ的旋轉,它的矩陣(對於這個標架說)是
再有,向著e
1的軸線所作係數為b/a的壓縮,它的矩陣是
.實際上,這個壓縮把向量e
1變成向量e'
1=1·e
1+0·e
3.把向量e
2變成向量
,而仿射變換矩陣的各個橫列正是向量e'
1,e'
2對向量e
1,e
2的分解式里的係數.因為σ
-1顯然是向著同一條軸線所作的係數為例數a/b的壓縮,所以σ
-1的矩陣是
,因此.按著公式(2),由普通的旋轉τ用壓縮σ誘發出來的橢圓旋轉τ',它的矩陣是矩陣乘積
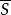
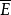
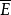
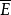
 圖1
圖1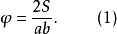


 圖2
圖2