基本介紹
- 中文名:非標準全域
- 外文名:nonstandard universe
- 適用範圍:數理科學
簡介


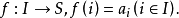




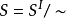
性質




公理
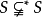


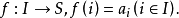




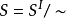




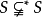
非標準全域是標準全域的非標準模型,它是另一個超結構的子集。非標準全域也可用公理方法建立。...
標準全域(standard universe)亦稱超結構,是一個包括力十分強的標準模型。...... 標準全域(standard universe)亦稱超結構,是一個包括力十分強的標準模型。...
非標準拓撲(nonstandard topology)是在非標準全域中展開的拓撲學。正像使用無限小數和無限大數可使微積分的基本概念更加直觀,推理更加簡明一樣,在非標準全域中展開...
標準定義原理是用可定義性判別標準集的一個定理。設B是非標準全域*U中的一個集合,則B是標準集若且唯若它是一個標準集的“標準”可定義子集,即集合B是標準的...
非標準泛函分析(nonstandard functional anal-ysis)建立在非標準全域上的泛函分析.非標準分析一出現,就在泛函分析方面取得了巨大的成就。...
內集是本身是非標準全域的元素的集合。由非標準全域的超冪構造可知,*U中的一個實體是內的若且唯若它可以表示為標準全域U中的一個有界序列。...
超有限集(hyperfinite set)亦稱*有限集,類似於有限集的內集。在超冪構造的非標準全域中,內集是超有限的若且唯若幾乎所有的(a.e.)Ai是有限的。...
設A是非標準全域*U中的一個子集,則A是內集若且唯若它是一個內集的可定義子集。內函式定理非標準全域 編輯 非標準全域是標準全域的非標準模型,它是另一個...
轉換原理亦稱萊布尼茨原理,是聯繫分析的標準模型與非標準模型的紐帶。...... 在用超冪構造的非標準全域中,可以證明轉換原理成立。在非標準全域的公理定義中,第二條...
超實數域(hyperreal number field)是實數域R在分析的非標準模型中的自然擴張,記為*R。...
B模型(B-model)也叫作B擴大。B模型是一種特殊的非標準模型。...... B模型亦稱B擴大,是一種特殊的非標準模型。...設R是標準全域U中的一個二元關係,若對R的...
5、標準USB擴展功能,滿足多USB設備使用者的需求。超極核X4 超極核X61、超極...2、可支持90-264Vac全域電壓輸入3、模組化設計4、強大的單路+12V輸出設計5、...
[3] 該方面明確指出要加強資源保護與規劃建設管理的全域全過程管控;加強省級規劃...統一用地分類,系統整合《土地利用現狀分類》、《城市用地分類與規劃建設用地標準》...
著力規劃和產業發展,科學定位"半島田園水鄉·有機生態小鎮",引進社會資金全域參與...為確保此次植樹活動不走過場,出實效,鎮領導不時檢查所挖的樹坑是否符合標準,...
