基本介紹
- 中文名:非標準拓撲
- 外文名:nonstandard topology
- 領域:數學
- 性質:拓撲學
- 定義:非標準全域中展開的拓撲學
- 意義:使拓撲學的基本概念更加直觀
簡介,定義,非標準全域,拓撲學,
簡介
非標準拓撲(nonstandard topology)是在非標準全域中展開的拓撲學。正像使用無限小數和無限大數可使微積分的基本概念更加直觀,推理更加簡明一樣,在非標準全域中展開拓撲學,使用單子及飽和性可使拓撲學的基本概念更加直觀,推理更加簡明。
定義
設(X,τ)是一個拓撲空間,其中X是任一非空集合,τ是X上的拓撲(τ是X的一些子集構成的族,空集和全集X屬於τ,並且τ對有限交和任意並封閉)。設空間X及實數集合R都是標準全域*V(S)的個體集S的子集。並設相應的非標準全域V(S)是多飽和的,即基數不超過標準全域*V(S)的基數並且具有有限交性質的內集族的全交非空。更確切地說,若Aj∈V(S),{Aj}j∈J具有有限交性質,並且J的基數≤card V(S),則∩{Aj}j∈J≠∅。此時,X在*V(S)中的自然擴張*X是X的一個合適的非標準模型。設a∈X,則*X的子集:
M(a)=∩{*O|a∈O並且O∈τ}
稱為a的單子。若x∈M(a),則稱x近於a或近標準於a。.所有近標準點的集合記為:
ns(*X)={x∈*X|∃a∈X,x∈M(a)}.
用單子可以成功地描述“鄰近”這個概念。由開集的定義可知,一個集合是開集若且唯若它的每一個點是它的內點(點a為集合A的內點,若且唯若A是a的一個鄰域,即存在O∈τ,使得a∈O⊂A),這反映了開集是包含它的每一個點的“鄰近”所有點的集合。使用單子概念,可以更直觀地說成:集合A是開集若且唯若*A中的每個標準點的單子包括*A中,即設A⊂X,A是開集若且唯若ᗄa∈A,M(a)⊂*A。事實上,若A是開集並且a∈A,則由單子的定義,M(a)⊂*A。反之,若A不是開集,則存在a∈A,a不是A的內點,即a的每個開鄰域O與A的余集的交非空:O∩Ac≠∅。顯然集族:
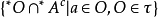
具有有限交性質。由多飽和性。
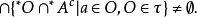
這個集合中的任一元素屬於M(a),但不屬於*A。
再如函式的連續性,它的直觀意義是把鄰近的點映為鄰近的點。標準的定義如下:設(X,T),(Y,U)是兩個拓撲空間,f:X→Y,f在點a連續,若且唯若對任意的U∈U(f(a))(f(a)的鄰域系),存在T∈T(a)(a的鄰域系),使得f(T)⊂U.這類似於用ε-δ來描述實連續函式。使用單子及飽和性可直接陳述為:f在點a連續,若且唯若:f(M(a))⊂M(f(a)),即把單子映到單子內。非標準方法在研究拓撲空間的緊性方面有更大的優點。可以證明,拓撲空間X是緊的若且唯若X的所有點是近標準點。這就把開集覆蓋的性質轉化為點集的性質.利用這個性質,很容易證明與緊性有關的定理,例如,吉洪諾夫定理——緊空間的乘積仍是緊空間。
非標準全域
非標準全域是標準全域的非標準模型。它是另一個超結構的子集。設U=V(S)是一個以S為個體集的標準全域,I為指標集(I可取自然數集或更大的集合),U為I上的一個自由超濾子,S是I到S的一切函式(I-序列)之集,即S={{ai}|ai∈S},其中{ai}表示I到S的一個函式f:I→S,f(i)=ai(i∈I).在S上定義等價關係:{ai}~{bi}若且唯若{i∈I|ai=bi}∈U.這個等價關係簡單地寫成ai=bi,a.e..令S=S/~,以S為個體集的超結構記為V(S)。
標準全域U=V(S)的非標準全域U=V(S)是V(S)的一個子集,它的元素按如下方式歸納地選自V(S)。設{Ai}是V(S)中元素的一個I序列,若存在一個p∈N,使得Ai∈Vp(S)(i∈I),則稱序列{Ai}是有界的。若序列{Ai}是有界的,則存在一個最小的j∈N,使得{i|Ai∈Vj(S)}∈U,這個j稱為序列{Ai}的秩。對於每個有界序列{Ai},可以按秩歸納地選取一個元素A∈V(S),並記A=〈Ai〉:若{Ai}的秩為0,令A=〈Ai〉,即S中的一個元素。假設對於秩小於j的每個序列{Bi}已經定義了對應的元素〈Bi〉,並且{Ai}的秩為j,則定義〈Ai〉={〈Bi〉|{Bi}的秩小於j,並且Bi∈Ai,a.e.}。這樣就完成了非標準全域U=V(S)的定義。V(S)中的元素稱為內的,V(S)\V(S)中的元素稱為外的.由上述定義,S中的元素都是內的,因而沒有外的個體。上述構造非標準全域的方法稱為超冪構造。
非標準全域也可用公理方法建立如下。設V(S)和V(S)分別是以S和S為個體集的兩個超結構,嵌入映射:V(S)→V(S)滿足如下兩條公理:
擴張原理 S是S的真擴張,即S⫋S,並且對於每個a∈S,有a=a。
轉換原理 標準全域的語言L(V(S))中的句子φ在V(S)中為真,若且唯若它的-轉換φ在V(S)中為真。φ是把φ中出現的常元符號a全部換成它的-像的符號a得到的句子。.若A∈V(S)\S,則A稱為標準集合,V(S)中的元素是內的,若且唯若它是某個標準集合的元素。所有內的元素構成的集合記為V(S),它就是標準全域V(S)對應的非標準全域。
拓撲學
現代數學的重要的分支學科。它研究幾何形體在連續形變,精確地說,雙方一一而且雙方連續的變換(稱為同胚)之下保持不變的性質。理解的廣泛些,它是研究數學中連續性現象的學科。
拓撲學萌芽很早,但直到19世紀末才開始從不同的方面正式形成學科。20世紀末,拓撲學已發展為現代數學的一個龐大的學科,包括作為現代數學的基礎的拓撲空間理論為核心內容的一般拓撲學,運用抽象代數的概念和方法為工具的代數拓撲學,進而派生出以流形為主要對象的微分拓撲學以及幾何拓撲學等方面。拓撲學可簡稱為拓撲,但拓撲一詞還可作為拓撲空間中的拓撲結構理解。
拓撲學最初被稱為形勢幾何學(geometria situs),這是萊布尼茨(Leibniz,G.W.)於1679年提出的,他預見到現在所稱的組合拓撲學。最早為人所知的拓撲學定理可能是所謂的歐拉公式。歐拉(Euler,L.)於1750年發表了任何閉的凸多面體的頂點數v,棱數e和面數f有關係v-e+f=2。用現代說法,它是一個拓撲不變數,稱為歐拉示性數。據史學家考證,笛卡兒(Descartes,R.)在1639年就知道它,並且萊布尼茨通過笛卡兒未發表的手稿於1675年得知這一結果。另一著名的結果是哥尼斯堡七橋問題的解決,歐拉在1736年將問題表成能否一筆畫一個給定的圖,並給出了一般性的解答.德國數學家高斯(Gauss,C.F.)於1827年得到曲面上曲率的積分與歐拉示性數的關係,他於1823年在電動力學中用線積分定義了空間中兩條封閉曲線的環繞數。利斯廷(Listing,J.B.)於1848年第一次採用了拓撲學一詞,其實他認為寧願用形勢幾何,只是已被別人采作他用。黎曼(Riemann,B.)於1851年定義了黎曼面,引進了連通性和虧格,實際上解決了可定向閉曲面的分類問題,給拓撲學的建立以巨大的推動。1858年,默比烏斯(Mo¨bius,A.F.)和利斯廷獨立地發現了單側的曲面,現被更確切地稱為不可定向曲面。默比烏斯於1863年恰當地指出形勢幾何學的定義。貝蒂(Betti,E.)於1870年定義了高維的連通性。若爾當(Jordan,C.)於1887年提出曲線定理,但證明是錯的,直到1905年才得證。
拓撲學正式成為一門獨立的學科是龐加萊(Poincaré,H.)實現的。他於1892年發表了題為“論形勢分析”的短文,然後於1895年發表了題為“形勢分析”的120頁的長文,介紹它的概念,其中有同調、貝蒂數、相交、基本群,甚至隱含著上同調;建立了對偶定理和歐拉-龐加萊公式。隨後直到1904年,他連續發表了五篇補充,為改進前述長文中的缺點創立了剖分方法,定義了撓係數,開始探討三維流形的拓撲分類,構造出基本群不平凡而一維貝蒂數平凡的三維流形,並提出了著名的至今尚未解決的龐加萊猜想:基本群平凡的三維閉流形同胚於三維球面。這幾篇文章奠定了組合拓撲學的基礎,其思想之豐富,觀念之深刻,影響之深遠,一言難盡,但不夠嚴密或缺乏證明,後來的進展正是從此入手,將這門學科建立在嚴格的邏輯上而發展為後來的組合拓撲學、代數拓撲學,進而發展出微分拓撲學等學科和分支。
