基本介紹
- 中文名:非旋場
- 外文名:Conservative vector field
- 別名:保守矢量場
定義,路徑無關,無旋矢量場,無旋流動,保守力,參見,
定義
一個矢量場 稱為保守的,如果存在一個標量場
稱為保守的,如果存在一個標量場 ,使得:
,使得:


矢量分析基本定理表明,任何一個矢量場都可以表示為一個保守矢量場和一個螺線矢量場的和。
路徑無關
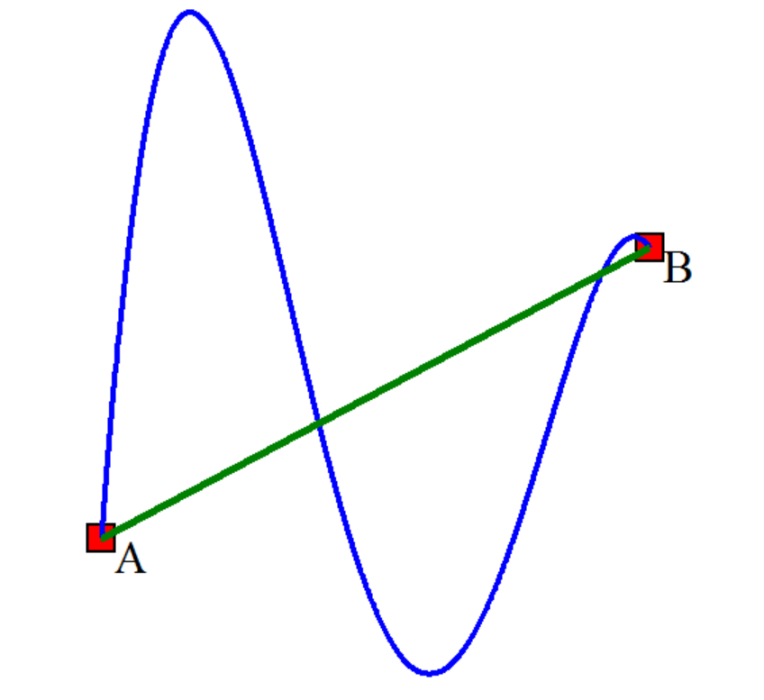
保守矢量場的一個重要性質是它沿著一條路徑的積分只與起點和終點有關,與路徑無關。假設 是三維空間內的一個區域,P是S內的一個可求長路徑,其起點為A,終點為B。如果
是三維空間內的一個區域,P是S內的一個可求長路徑,其起點為A,終點為B。如果 是保守矢量場,那么:
是保守矢量場,那么:


一個等價的表述是,對於S內的所有閉合路徑,都有:
無旋矢量場
矢量場 是無旋的,如果它的旋度是零,也就是說:
是無旋的,如果它的旋度是零,也就是說:


由於這個原因,這種矢量場有時稱為無旋矢量場。
對於任何標量場 ,都有:
,都有:


因此保守矢量場都是無旋矢量場。
只要S是單連通區域,它的逆命題也是成立的:每一個無旋矢量場也都是保守矢量場。
如果S不是單連通的,則逆命題不成立。設S為去掉z軸的三維空間,也就是 。現在,我們定義以下的矢量場:
。現在,我們定義以下的矢量場:








更加抽象地,保守矢量場是恰當1-形式。也就是說,它是一個1-形式,等於某個0-形式(標量場) 的外導數。一個無旋矢量場是閉合1-形式。由於d= 0,任何正合形式都是閉合的,因此任何保守矢量場都是無旋的。定義域是單連通的,若且唯若它的第一個同調群為零,或第一個上同調群為零。第一個德拉姆上同調群
的外導數。一個無旋矢量場是閉合1-形式。由於d= 0,任何正合形式都是閉合的,因此任何保守矢量場都是無旋的。定義域是單連通的,若且唯若它的第一個同調群為零,或第一個上同調群為零。第一個德拉姆上同調群 是零,若且唯若所有閉合1-形式都是恰當的。
是零,若且唯若所有閉合1-形式都是恰當的。


無旋流動
流體的流速 是矢量場,它的渦度
是矢量場,它的渦度 通常由以下公式定義:
通常由以下公式定義:



如果是無旋的,那么這個流動就稱為無旋流動。無旋流動的渦度是零。
對於二維流動,渦度是流體元素的局部旋轉的一種衡量。注意渦度並不能說明流體的整體表現。做直線運動而具有渦度的流體是有可能的,做圓周運動而是無旋的流體也是有可能的。關於更多信息,請參見旋渦。