複平面上的一個區域G,如果在其中任做一條簡單閉曲線,而閉曲線的內部總屬於G,就稱G為單連通區域。一個區域如果不是單連通區域,就稱為多連通區域。
基本介紹
- 中文名:連通區域
- 外文名:connected domain
- 分類:單連通、多連通
- 區分:是否有“洞”
- 領域:複平面上的拓撲基本概念
- 學科:數學
定義
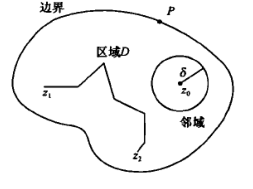 圖1 區域
圖1 區域
複平面上的一個區域G,如果在其中任做一條簡單閉曲線,而閉曲線的內部總屬於G,就稱G為單連通區域。一個區域如果不是單連通區域,就稱為多連通區域。
 圖1 區域
圖1 區域
複平面上的一個區域G,如果在其中任做一條簡單閉曲線,而閉曲線的內部總屬於G,就稱G為單連通區域。一個區域如果不是單連通區域,就稱為多連通區域。...
設D是一區域,若屬於D內任一簡單閉曲線的內部都屬於D,則稱D為單連通區域,單連通區域也可以這樣描述:D內任一封閉曲線所圍成的區域內只含有D中的點。更通俗地...
八向連通(八連通)區域指的是從區域內每一象素出發,可通過八個方向,即上、下、左、右、左上、右上、左下、右下這八個方向的移動的組合,在不越出區域的前提...
多連通域是指複平面上的一個區域B,如果在其中存在一條簡單連續閉曲線,而曲線的內部不屬於B。...
像素間的連通性是一個基本概念,它簡化了許多數字圖像概念的定義,如區域和邊界。為了確定兩像素是否連通,必須確定它們是否相鄰以及其灰度值是否滿足特定的相似性準則(...
區域是一個漢字詞語,讀音為qū yù,是指土地的界劃;地區區域自治。指國家管轄範圍以外的海床和洋底及其底土。語出《周禮·地官·序官》“廛人” 漢 鄭玄 ...
閉區域(closed region)是指簡單閉曲線及它的內部,構成“平面閉區域”。類似地,可定義空間閉區域。也稱區域與它的邊界的並集稱為閉區域。區域(region)是幾何學的...
區域模型是把地理空間中的現象作為連續的變數或體來看待,如大氣污染程度、地表溫度、土壤濕度、地形高度以及大面積空氣和水域的流速和方向等。根據不同的套用,模型...
將一幅圖像分割成不同區域後,使用更適合於計算機進一步處理的形式,對得到的被分割的像素集進行表示和描述。因此,圖像表示與描述是圖像識別和理解中的重要工作。區域...
連線召喚是《遊戲王》召喚方式之一。是連線怪獸從額外卡組出場的正規召喚方式。在新大師規則的遊戲規則變更下,連線怪獸擁有的「連線標記」能把主要怪獸區域變成額外...
弧連通集(arcwise connected set)亦稱路徑連通集,可用弧連結其中任意兩點的點集,對於平麵點集情形指它是這樣的:若E⊂R2,若對於E中任意的兩點(a,x)和(b,y)...
連通運河(connection canal)是指連通互不銜接的水系的運河。如中國的京杭運河。京杭大運河始建於春秋時期。春秋戰國時期開鑿運河基本都是為了征服他國的軍事行動服務...
區域生長(region growing)是指將成組的像素或區域發展成更大區域的過程。從種子點的集合開始,從這些點的區域增長是通過將與每個種子點有相似屬性像強度、灰度級、...
區域預報,指土地的界劃預報。區域語出《周禮·地官·序官》"廛人" 漢 鄭玄 注:"廛,民居區域之稱。"...
《連通電路》是一款益智類網頁遊戲。...... 滑鼠點擊旋轉物體使電流順利到達各個區域激活整個電路。[1] 參考資料 1. 連通電路 .4399小遊戲[引用日期2014-08-03]...
正則集是經典的狄利克雷域的推廣。一個區域如果是正則集,就稱為正則區域(regular domain)。...
超級區域是超過50%的全球人口居住在城市。由於“超級區域”的快速形成,這個數字將在不到20年的時間裡上升至70%。聯合國每年發表兩次的《世界城市現況報告》(State ...
斯米爾諾夫區域是一種與多項式系完備性相關的區域。使多項式系在Ep(G)中完備的充分必要條件是,區域G為斯米爾諾夫區域。...
中信證券分析師張兵表示,電信業已處於歷史估值底部區域,3G及增值業務將是今年運營商價值增長的實質性推動因素。聯通WCDMA套用現狀 編輯 淺談聯通3G對WCDMA的套用現狀與...
城區是指人口、機構、經濟、文化、高度集中的區域。與“郊區”而相對。...... 市轄區和不設區的市,區、市政府駐地的實際建設連線到的居民委員會所轄區域和其他...
ABR是位於一個或多個OSPF區域邊界上、將這些區域連線到主幹網路的路由器。...... ABR是位於一個或多個OSPF區域邊界上、將這些區域連線到主幹網路的路由器。...
填充算法是計算機算法的一種分類,是一個將指定不規則區域內部像素填充為填充色的過程,在計算機輔助設計和圖像處理等領域有廣泛套用。包括了注入填充區域算法、種子填充...
一個基本域是這個空間的一個子集,包含了每個軌道中恰好一點。基本域具體地用幾何表現出抽象的軌道代表集。 構造基本域的方法有很多。一般會要求基本域是連通的,...
