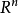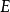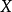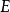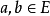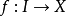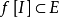弧連通集

弧連通集(arcwise connected set)亦稱路徑連通集，可用弧連結其中任意兩點的點集，對於平麵點集情形指它是這樣的：若E⊂R²，若對於E中任意的兩點(a，x)和(b，y)，存在區間[a，b]上的連續單調函式f，使得f(a)=x，f(b)=y，則稱E為弧連通集。弧連通集必是連通的，反之不一定，例如，平面曲線y=sin(1/x)，(0<x≤1)，與x軸上的線段-1≤x≤0的並集是連通的，但不是弧連通的。在Rⁿ中，連通的開集是弧連通的。Rⁿ的凸子集總是弧連通的，因而是連通的。當所用的弧是折線，即有限條線段的並集時，弧連通集稱為折線連通集。在Rⁿ中，連通開集是折線連通的。n維球、n維區間、n維球面都是弧連通的。

基本介紹

• 中文名：弧連通集
• 外文名：arcwise connected set
• 別稱：路徑連通集
• 所屬學科：數學
• 所屬問題：數學分析(實數理論)

定義介紹

設為拓撲空間的一個子集，如果對於中的任何兩點，都有一條含在E中而由a到b的道路(即)，則稱E為一個弧連通集(arcwise connectedset)。

中的極大的弧連通集稱為一個弧連通的分支(arcwiseconnected component)，X中所有的弧連通分支構成X的一個分割。

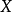
相關定理

弧連通與連通之間有以下關係：

定理1弧連通集是連通的。

上述定理的逆命題是不成立的，如下面例題所示。

例1考察平面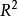上的子集：

其中A是由所有連結原點與點的線段上的點所組成；B是由軸上與1之間的一切點所組成。現在A與B都是弧連通的，因而也是連通的；另外，A與B又是不互相分離的，因為每點都是A的一個極限點。於是是連通的。但卻不是弧連通的，因為實際上不存在A上任何一點到B上任何一點的道路。

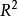
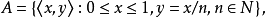
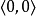
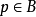
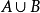
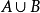
圖1

平面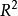上的拓撲學是單變數複函數論的一個重要部分。在複函數論中，把平面上的開連通集稱為一個區域(region)，下面的定理在複函數論中是重要的。

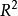
定理2平面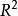上的開連通集是弧連通的。

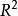
弧連通空間

若拓撲空間上任意兩點可由其上的弧連線(即此弧分別以這兩點為起點和終點)，則稱此空間為弧連通的，若空間有一由弧連通集組成的基，則稱為局部弧連通空間。

局部弧連通空間是弧連通的若且唯若是連通的。

是局部弧連通的。