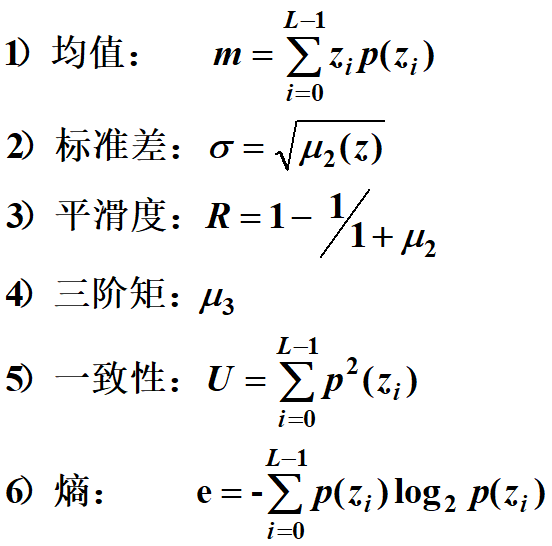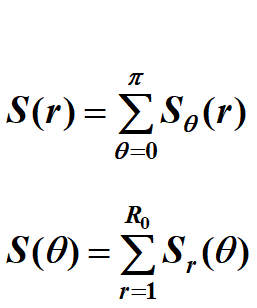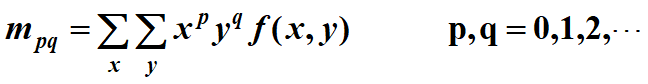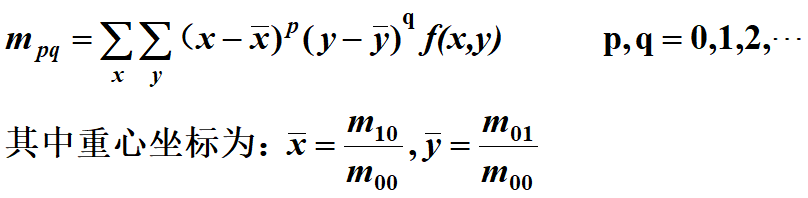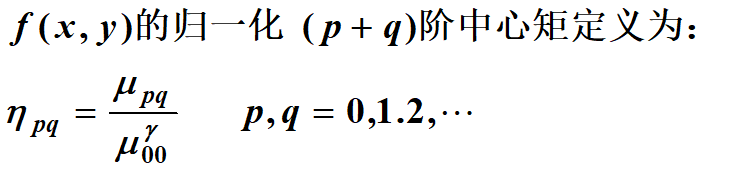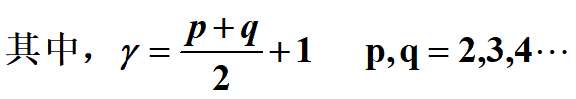將一幅圖像分割成不同區域後,使用更適合於計算機進一步處理的形式,對得到的被分割的像素集進行表示和描述。因此,圖像表示與描述是圖像識別和理解中的重要工作。
區域表示關注的是圖像中區域的的灰度、顏色、紋理等特徵,常用的方法有四叉樹、骨架等。
骨架
把平面區域抽取為圖形的一種區域表示方法,通過使用一種細化(也稱骨架)算法得到區域。一個區域的骨架可以用中軸轉換方法(MAT)定義。
設區域R的邊界為B,對R中的每一點p,找到它在B上最接近的鄰點。如果p有多於一個這樣的鄰點,就認為p屬於R的中軸(骨架)。“最接近”取決於距離的定義。
中軸變換特點:
MAT是一種很直接的細化方法,但是需要計算區域內部每一點其邊界點的距離,所以計算量很大。
改進的骨架求取算法包括基於形態學的方法。
區域的形狀描述
當關注區域的形狀特徵時常採用邊界描述。邊界描述方法包括簡單的描述子,形狀數,付里葉描述子和統計矩等。
邊界長度
一條邊界所包圍的區域輪廓的周長就是邊界長度。對4連通邊界,其長度為邊界上像素點個數;對8連通邊界,其長度為水平和垂直像素點的個數再加上對角線像素點的個數乘以√2。
邊界的直徑
邊界的直徑是邊界上任意兩點的最大值,即
一般,直徑的值和連線直徑的兩個端點的直線段稱為邊界的長軸;與長軸垂直的直線為邊界線的短軸;長軸和短軸的比值為邊界線的離心率。
形狀數
形狀數是基於4鏈碼的邊界描述符,它定義為值最小的4鏈碼的一階差分碼。
一個形狀數的階數n定義為其表達形式中的位數。
例:
鏈碼:00300323222121101
一階差分碼:30310331300313031
形狀數:00313031303103313
注意:儘管鏈碼的最小一階差分碼(形狀數)與起始點無關,且獨立於旋轉變化,但是總體上編碼邊界依賴於格線的取向。
任意旋轉角度的歸一化:
通常採用的方法是將一個坐標軸(如x軸)與邊界的主軸對齊。
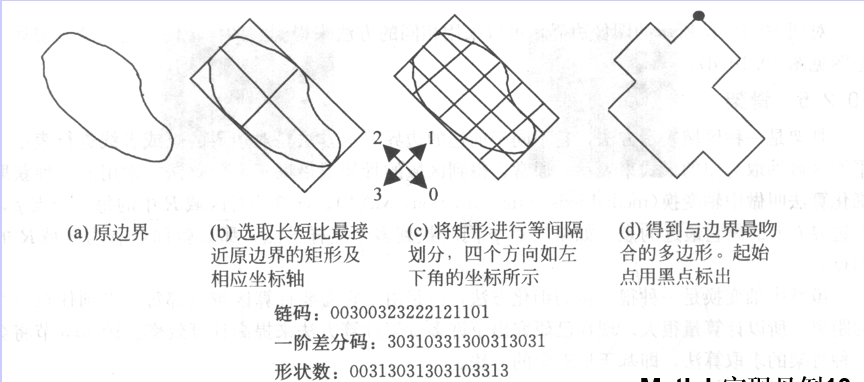 圖4 獲取形狀數的步數
圖4 獲取形狀數的步數格線的歸一化:
區域的長軸和短軸與邊界4個外側交點的方框定義為基本矩形,它完全包圍了邊界的軸線。因此,可以使用基本方框設定格線尺寸。
區域內部描繪
當關注圖像中的區域內部特徵(如
顏色特徵、紋理特徵等)時,一般會採用區域內部描述方式。
區域面積
一個區域的面積定義為區域中像素的數目。
區域重心
區域重心是一種全局描述符,區域重心的坐標是根據所有屬於區域的點計算出來的,計算公式如下:
注意:
1)儘管區域各點的坐標總是整數,但區域重心的坐標常常不是整數;
2)對於非規則物體,其重心坐標和幾何中心坐標常常不相同。
紋理
目前對紋理無正式定義。紋理可以被認為是:
1)灰度(顏色)在空間以一定的形式變化而產生的 圖案(模式)。
2)由許多相互接近的、互相編織的元素構成(它們 常常有周期性)。
3)在視場範圍內的灰度分布模式。這是一種可操作 的定義。常用矢量表達。
紋理特徵:
1)直觀特性:提供圖像區域的平滑、稀疏、規則性等;
2)心理學特性:紋理特徵包括粒度、方向性、重複性等;
3)頻率特性:紋理和圖像頻譜中的高頻分量的聯繫
一般,紋理圖像中的灰度分布具有
周期性,既使灰度變化是隨機的,也具有一定的統計特性。
紋理可分為人工紋理和自然紋理。人工紋理是由自然背景上的符號排列組成,這些符號可以是線條、點、字母、數字等。
自然紋理是具有重複性排列現象的自然景象。
 人工紋理與自然紋理
人工紋理與自然紋理紋理檢測:
在圖像處理中用於描述區域紋理的3種主要方法是:統計方法、結構化方法和頻譜方法。
最簡單的方法是取灰度值的一階、二階微分的平均值與方差;如果考慮紋理的方向性,則可以計算方向差分的平均值與方差。
還可以利用灰度直方圖來確定紋理目標。即檢查各小區域圖像的直方圖的相似性,具有相似直方圖的小區域同屬於一個大區域,而直方圖不同的小區域屬於不同的區域。
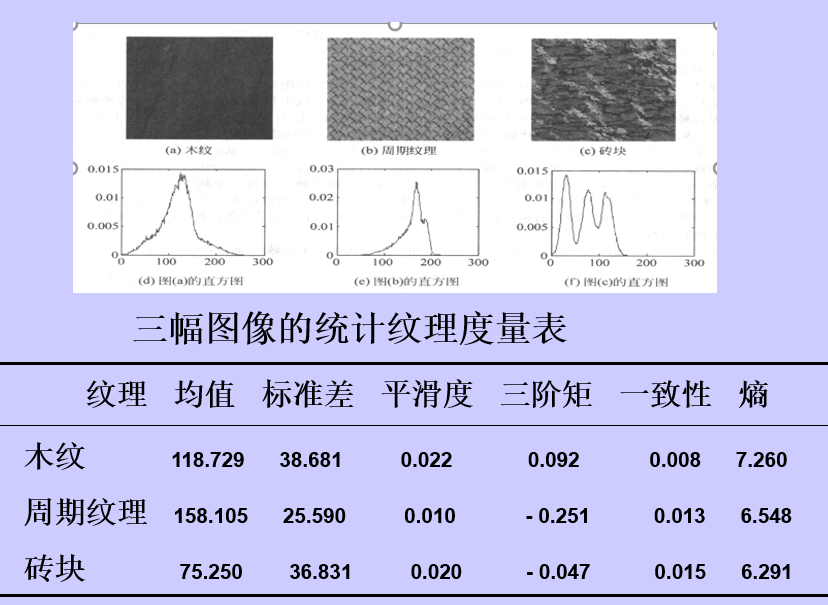
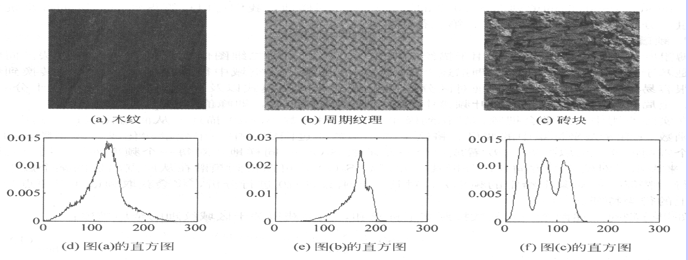 紋理圖像
紋理圖像統計方法指諸如平滑、粗糙、粒狀等紋理的特徵描述。結構化技術處理圖像元的排列,諸如基於均勻空間分布的平行線紋理描述,用句法結構方法(如:描述各個像素及其鄰近像素的灰度分布情況)。
頻譜技術基於傅立葉頻譜特性,主要用於通過識別頻譜中高能量的窄波峰尋找圖像中的整體周期性。
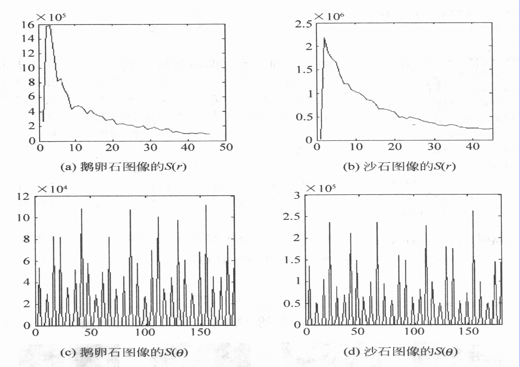 紋理圖像的頻譜特徵
紋理圖像的頻譜特徵統計法
在統計法中,紋理被看作一種對區域中密度分布的定量測量結果。統計模型是利用圖像灰度的分布和關係的統計規則來描述紋理。
它比較適合描述自然紋理,一般可提供紋理的平滑 、稀疏、規則等性質。
最簡單方法之一是使用一幅圖像或區域灰度級直方圖的統計矩。
設圖像的灰度級為L,灰度的隨機數為zi,p(zi)為區域灰度直方圖,則灰度均值m的n階矩表達式為:
常用的紋理統計量有(L為圖像的灰度級數):
頻譜法
基於傅立葉頻譜的一種紋理描述方法。它是一種理想的可用於描述周期或近似周期的二維圖像模式的方向性的方法。通常,全局紋理模式對應於傅立葉頻譜中能量十分集中的區域,即峰值突起處。
區域紋理的全局描述:
不變矩
不變矩是描述區域的方法之一。
區域f(x,y)的(p+q)階矩定義為:
中心矩定義為:
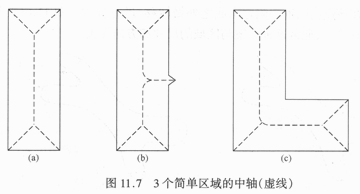

 圖4 獲取形狀數的步數
圖4 獲取形狀數的步數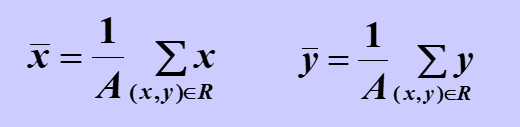
 人工紋理與自然紋理
人工紋理與自然紋理 紋理圖像
紋理圖像 紋理圖像的頻譜特徵
紋理圖像的頻譜特徵