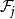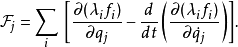非完整系統

在古典力學裡，假如，一個系統有任何約束是非完整約束，則稱此系統為非完整系統。非完整約束不是完整約束。

基本介紹

• 中文名：非完整系統
• 外文名：Nonholonomic system
• 定義：一個系統有任何約束是非完整約束
• 相關術語：完整約束
• 學科：古典力學
• 領域：力學

定義

在古典力學裡，假如，一個系統有任何約束是非完整約束，則稱此系統為非完整系統。非完整約束不是完整約束。完整約束可以用方程式表示為

這裡，f是每一個粒子 之位置和時間的函式。非完整約束不能夠用上述方程式表示。

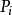
廣義座標轉換

完整約束方程式與位置、時間有關，與速度無關。完整約束方程式可以很簡易地除去指定的變數。假設變數x_d是完整約束函式f_k里的一個參數，現在指定除去 x_d。重新編排上述約束方程式，求出表示x_d的函式g_k：

將函式g_k代入所有提到x_d的方程式。這樣，可以除去所有指定變數x_d。

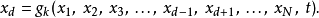
假設一個物理系統原本的自由度是N。現在，將h個完整約束作用於此系統。那么，這系統的自由度減少為m=N-h。可以用m個獨立廣義座標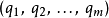 來完全描述這系統的運動。座標的轉換方程式可以表示如下：

換句話說，由於非完整約束無法依照上述方法，來除去其所含廣義座標，完全描述非完整系統，所需要的廣義座標數目，大於自由度。

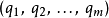
微分形式表示

約束有時可以用微分形式的約束方程式來表示。思考第i個約束的微分形式的約束方程式：

這裡， 分別為微分 的係數。

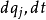
假若此約束方程式是可積分的。也就是說，有一個函式 的全微分滿足下述等式：

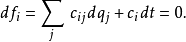
那么，此約束是完整約束；否則，此約束是非完整約束。因此，所有的完整約束與某些非完整約束可以用微分形式的方程式來表示。不是所有的非完整約束都可以這樣表示。含有廣義速度的非完整約束就不能這樣表示。所以，假若知道一個約束的微分形式的約束方程式，這約束到底是完整約束，還是非完整約束，需要看微分形式的約束方程式能否積分來決定。

半完整系統

表示非完整約束的方程式往往比較複雜。因此，非完整系統也比較難分析，只有簡易一點的非完整系統能用形式論來分析。假如，一個非完整系統的約束可以用以下方程式表示：

則稱此系統為半完整系統；這裡， 是廣義速度。

半完整系統可以用拉格朗日形式論來分析。更具體地說，分析半完整系統必須用到拉格朗日乘子

這裡， 是未知函式。

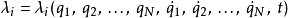
假設哈密頓原理成立，則下述方程式成立：

這裡，L是拉格朗日量， 分別為積分的時間下限與上限。經過變分法運算，可以得到方程式

由於這N個廣義座標中，仍舊有n個不獨立廣義座標，不能將拉格朗日方程式提取出來；必須加入拉格朗日乘子項目：

經過變分法運算，可以得到方程式

這裡， 是廣義力的j分量：

雖然還有n個不獨立廣義座標，仍舊可以調整n加入的拉格朗日乘子，使總和公式內的每一個虛位移 的係數都等於0。因此，

這N個方程式加上n個約束方程式，給予了N+n個方程式來解N個未知廣義座標與n個拉格朗日乘子。

實例

非完整系統至少存在於以下三個狀況：

1. 物體在做滾動運動。
   
2. 系統的約束包括不等式。
   
3. 系統的約束與速度有關（例如普法夫約束）。