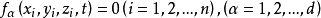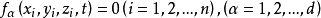如果約束方程中不包含坐標對時間的導數，或者約束方程中微分項可以積分為有限形式，這類約束稱為完整約束。
基本介紹
- 中文名：完整約束
- 外文名：holonomic constraint
- 不利用方程：動力學方程
- 利用方法：積分
簡介,實例,性質,推廣,
簡介
完整約束是指幾何約束和可積分的微分約束的統稱。前者如質點被限制在的圓環上，約束條件是半徑和圓心；後者如圓盤在平面上沿直線作無滑動的滾動。
如果約束方程中不包含坐標對時間的導數，或者約束方程中微分項可以積分為有限形式，這類約束稱為完整約束。
實例
在車輪沿直線軌道做純滾動的情況中，其運動約束方程
雖是微分方程的形式，但它可以積分為有限形式，所以仍是完整約束。
性質
幾何約束必定是完整約束，但完整約束未必是幾何約束。
完整約束方程的一般形式為：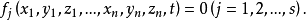
式中，n為質點系的質點數；s為約束方程數。
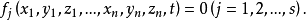
推廣
如果質點系所受的約束都是完整約束，這個質點系稱為完整系統，簡稱完整系。設某質點系由n個質點組成，內有d個完整約束，約束方程的有限形式和微分形式分別為
