零態射

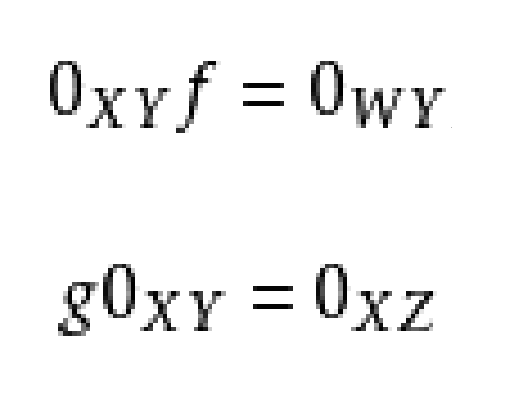
零態射(zero morphism)是有零對象的範疇中的一類特殊態射。許多常見範疇，如群範疇、環範疇、環模疇等，將它們的零同態概念抽象出來即得零態射的概念，它在範疇論中起著相當重要的作用。設範疇C有零對象(在等價意義下必惟一)Z，Hom(A，Z)與Hom(Z，B)的惟一元素分別為0_AZ和0_ZB。其合成0_ZB0_AZ不隨Z的選擇而改變，記此合成為0_AB，稱為Hom(A，B)中的零態射，對取定的A，B，這是惟一的，有時也簡記為0。

基本介紹

• 中文名：零態射
• 外文名：zero morphism
• 所屬學科：數學（範疇論）
• 性質：有零對象的範疇中的一類特殊態射
• 相關概念：零對象、範疇、對偶原則等

基本介紹

若範疇有零對象，則在同構意義下是唯一的。設Z是任意一個零對象，與為與中唯一的元素，則乘積不隨零對象的選取而改變。

通常以來表示乘積，這裡Z是任一零對象，這個叫作中的零態射。

零對象與零態射

定義

定義1 若對任何對象一定是單元集( 即僅含有一個元的集合)，則叫作始對象；若對任何對象一定是單元集，則叫作終對象； 若Z既是始對象又是終對象，則Z稱為零對象。

始對象與終對象是相互對偶的概念。

定義2設是一個範疇。

1)如果如果滿足：對於任意的恰由一個元素組成，則稱A 為中的一個初始對象；

2)如果對於任意的恰由一個元素組成，則稱A 為中的一個末端對象；

3)如果A 既是中的初始對象，又是末端對象，則稱A 為的一個零對象。

如果有零對象，則稱為具有零對象的範疇。

設為具有零對象0的一個範疇，X 和Y 是中任意兩對象，則有唯一的態射

和

於是，有複合態射

即

態射稱為零態射，記為。

例題解析

例1在中是一個初始對象；任一單元素集是一個末端對象；但無零對象。

例21)平凡(即一個元素的)BCK-代 數 是中 的一 個零對象；

2)平凡BCI-代數是中的一個零對象；

3)平凡BCH-代數是 中的一個零對象；

4)平凡(2,0)型代數是中的一個零對象；

5)平凡群是中的一個零對象。

例3在A(2,0)中，零態射正是通常的零同態映射。在及中都可得到此類似結果，這正是將稱為零態射的一個原因。

相關定理

定理1 假若是在範疇中的一個零態射，那么且。

定理2在一個範疇中的始對象與終對象是對偶的，從而零對象是自對偶的。

證明：設表示範疇中始對象的定義。於是： 是中的始對象,假若對於中的每一X，恰有一個成員。

：是中驗始對象，假若對於中的每一對象X，恰有一個成員。

：是中的終對象，假若對於中的每的X，恰有一個。

定理3 在一個範疇中，一切初始對象是同構的，一切末端對象是同構的；如果有零對象，則一切零對象是同構的。

定理4設是具有零對象0的一個範疇，則對於中的任何態射和有

且

證明：證(1)中第一式。由圖1，其中和分別是和中唯一的態射，且，顯然，，從而，

2) (1)中第二式可類似地證明。