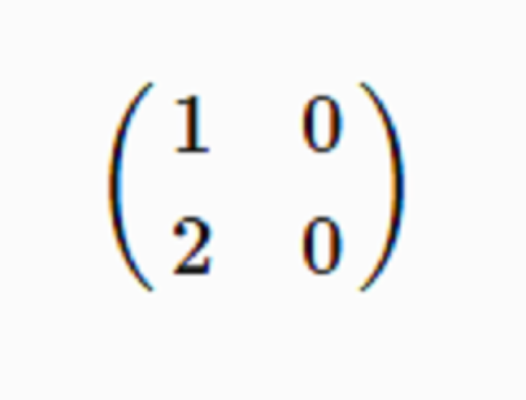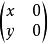零因子

零因子，亦稱零除元，環的一種特殊的非零元。環R中一個元a≠0，若有0≠b∈R使得ab=0或ba=0，稱a是環R的零因子，在非交換環中有左、右零因子之分，如上ab=0時，a稱左零因子；ba=0時，a稱右零因子。若環R有零因子，則消去律不成立；與零因子意義完全相反的元，即不是零因子的非零元，稱為正則元。數環沒有零因子，但在其它環 (如矩陣環)里零因子卻可能存在，域中不存在有零因子。

基本介紹

• 中文名：零因子
• 外文名：zero divisor
• 別名：零除元
• 屬性：環的一種特殊的非零元
• 分類 ：左零因子、右零因子

定義

眾所周知，在數的普通乘法中，如果a≠0，b≠0，則必有ab≠0，但這一性質在一般環中不再成立。

設a≠0是環R的一個元素，如果在R中存在元素b≠0使ab=0，則稱a為環R的一個左零因子，同樣可定義右零因子。

左、右零因子統稱為零因子，只在有必要區分時才加左或右。

既不是左零因子也不是右零因子的元素，稱為正則元。

例題解析

例1 設R為由一切形如

的方陣關於方陣的普通加法與乘法作成的環,其中x，y為有理數，則 是R的一個左零因子，因為有

但 不是R的右零因子，因為若

則只有 。

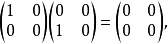
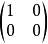
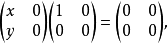
例2 數域F上二階全陣環中， 既是左零因子又是右零因子，因為有

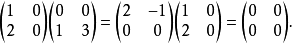
數環以及數域上的多項式環，都無零因子。

在無零因子的環中，關於乘法的消去律成立。

相關概念

整環階大於1、有單位元且無零因子的交換環稱為整環。

例如，整數環和數域上的多項式環都是整環，而例1和例2中的方陣環都不是整環，整環的定義在不同的書中往往稍有差異，請予留意。

特徵數 若環R的元素(對加法)有最大階n，則稱n為環R的特徵(或特徵數)，若環R的元素(對加法)無最大階，則稱R的特徵是無限（或零）用char R表示環R的特徵。

由於有限群中每個元素的階都有限，故有限環的元素對加法有最大階，從而有限環的特徵必有限，但是，無限環的特徵也可能有限，顯然，一階環即僅包含零元素的環，其特徵是1。而在數環中，除去{0}外，其特徵均無限。一般來說，環中各元素(對加法)的階是不相等的，但對無零因子的環來說，這種情況不會發生。

相關定理與性質

定理1

在環R中，若a不是左零因子，則

若a不是右零因子，則

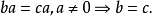
證明 由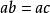 得

由於a≠0且a不是左零因子，故b-c=0，b=c。

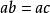
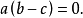
同理可證另一結論。

如果對環R中任意元素a≠0，b，c，(1)成立，則稱環R滿足左消去律；若(2)成立，則稱R滿足右消去律。

推論

若環R無左(或右)零因子，則消去律成立；反之，若R中有一個消去律成立，則R無左及右零因子，且另一個消去律也成立。

證明 由於當R無左零因子時，R也無右零因子，故由定理1即得消去律成立，反之，設在R中左消去律成立，且

即

則b=0，即R無左零因子，從而R也無右零因子，於是右消去律也成立。

定理2

設R是一個無零因子環，且 ，則

1)R中所有非零元素(對加法)的階均相同；

2)若R的特徵有限，則必為素數。

由此定理知，特別地，任何階大於1的有限環若無零因子，則其特徵都是素數。

如果環R的特徵是素數p，且R又是一個交換環，則對R中任意元素 必有

這是因為將 展開後，除去項 外其餘各項的係數都是p的倍數，從而都是R的零元。

等式 顯然是與數的普通運算規則很不一樣的一個等式。

當環有單位元時其特徵更明顯。

定理3

若環R有單位元，則單位元在加群(R，+)中的階就是R的特徵。

證明 若單位元1在(R，+)中的階無限，則R的特徵當然無限；若1的階是正整數n，則在R中任取a≠o，有

即n是R中非零元素的最大階，亦即