離散賦值是一種特殊的賦值,即值域為實數集的離散子集的非阿基米德賦值。離散賦值環對應於離散賦值。設(R,m)是一個維數為1的諾特局部環,如果m可以由一個元素生成,則稱R是離散賦值環。離散賦值環一定是整環。
基本介紹
- 中文名:離散賦值
- 外文名:discrete valuation
- 所屬學科:環論
- 定義:一種特殊的賦值
定義
定義1
定義2
簡介


離散賦值環




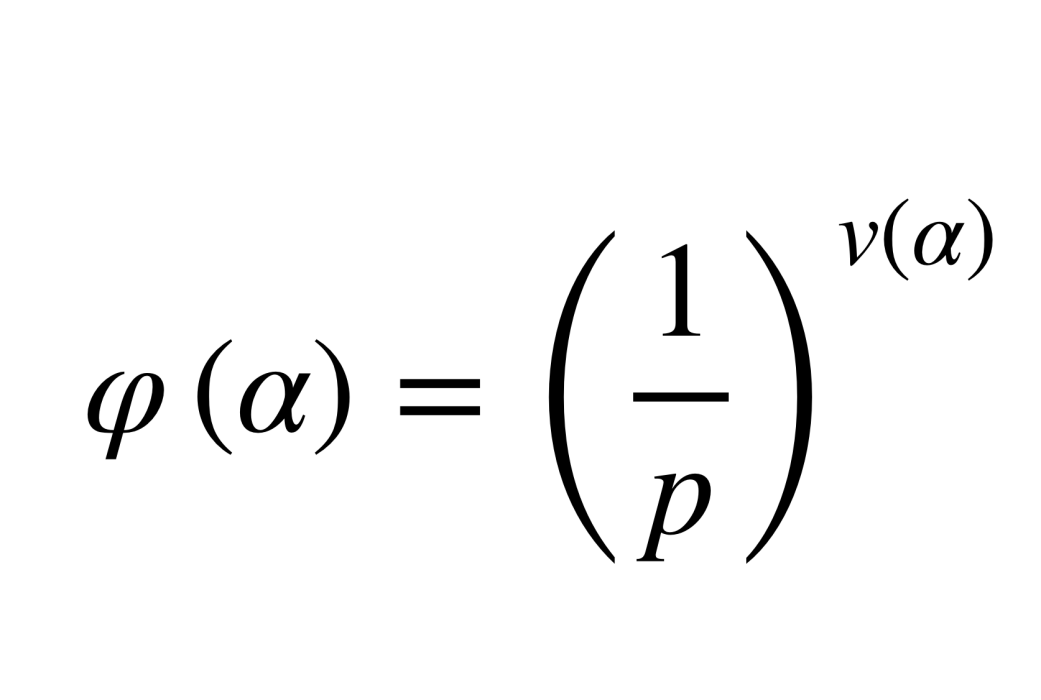
離散賦值是一種特殊的賦值,即值域為實數集的離散子集的非阿基米德賦值。離散賦值環對應於離散賦值。設(R,m)是一個維數為1的諾特局部環,如果m可以由一個元素生成,則稱R是離散賦值環。離散賦值環一定是整環。






離散賦值是一種特殊的賦值,即值域為實數集的離散子集的非阿基米德賦值。離散賦值環對應於離散賦值。設(R,m)是一個維數為1的諾特局部環,如果m可以由一個元素生成,則稱R是離散賦值環。離散賦值環一定是整環。定義定義1若賦值v...
一階離散賦值 一階離散賦值(discrete valuation of rank one)一種值群為整數加群的賦值。設F為一個域,φ為F'上的賦值.若φ的值群為整數加群,則稱φ為F的一階離散賦值.
9、離散賦值定義 設A為一個命題公式, 為出現在A中的所有的命題變項,給 指定一組真值,稱為對A的賦值或解釋,若指定的一組值使A值為真,則稱這組為A的成真賦值,若使A的值為假,則稱這組值為A的成假賦值 。10、賦值的...
《離散賦值環上的模》是2017年世界圖書出版公司出版的著作,作者是P.A.克雷洛夫(俄羅斯)、A.A.,圖根巴夫 。內容簡介 《離散賦值環上的模》向讀者呈現了離散賦值環上的模理論的概念、方法和定理,指出了離散賦值環和Abelian群之間的...
2.1 命題與聯結詞41離散數學目錄2.1.1 命題與真值41 2.1.2 命題聯結詞42 2.2 命題公式、指派及真值表46 2.2.1 命題公式46 2.2.2 命題的符號化 47 2.2.3 公式的指派(賦值)及真值表48 2.3 命題公式的等值式,蘊含...
1.2 命題公式與賦值 1.3 等值演算 1.4 權取範式與合取範式 1.5 命題邏輯的推理理論 1.6 例題分析 習題一 第二章 一階邏輯 2.1 一階邏輯的基本概念 2.2 一階邏輯公式及解釋 2.3 一階邏輯等值式與前束範式 2.4 一階...
1.2.1命題公式及賦值 1.2.2命題公式類型與真值表 1.3命題公式的等價演算 1.3.1命題公式的等價式 1.3.2命題公式的等價演算 1.3.3等價演算的實例套用 1.4命題公式的範式及套用 1.4.1析取範式與合取範式 1.4.2主析取範式...
1.2.3公式的賦值及真值表8 1.3命題公式的等值演算10 1.3.1命題公式的等值式10 1.3.2代入規則與替換規則11 1.4範式13 1.4.1合取範式與析取範式13 1.4.2主範式15 1.5聯結詞完備集18 1.6命題演算的推理理論20 1.7自然...
1.2 命題公式及其賦值 1.3 等值式 1.4 析取範式與合取範式 1.5 實驗一 1.6 推理理論 1.7 消解法 1.8 實驗二 綜合練習 第2章 謂詞邏輯 2.1 基本概念 2.2 謂詞公式及其解釋 2.2.1 合法的謂詞公式 2.2.2 ...
指數賦值(exponential valuation)是非阿基米德賦值的又一記法。設a是域F的非阿基米德賦值,對F中的a,若二(Cad = loga},則映射二:F'-> RU{二}稱為域F的一個指數賦值。含義 對任意a,bEF,有:若v(F)是R的離散加法子群,則稱...
1.2 命題公式與賦值 1.3 等值演算 1.4 析取範式與合取範式 1.5 命題邏輯的推理理論 1.6 典型例題分析 本章小結 習題 第2章 謂詞邏輯 2.1 謂詞邏輯的基本概念 2.2 謂詞公式與翻譯 2.3 謂詞演算的等價式與蘊涵式 2...
《離散數學(第2版)》是由屈婉玲、耿素雲、張立昂主編,2015年由高等教育出版社出版的普通高等教育“十一五”國家級規劃教材。該教材可作為普通高等學校計算機科學與技術、軟體工程、信息與計算科學等專業本科生離散數學課程教材,也可以供...
分解矩陣(decomposition matrix)群表示論的一個特殊矩陣.即描述與各個不可約常表示相應的模表示的不可約成分重數的矩陣.設R是一個完備的離散賦值環,K是R的分式域,k=R/J (R)是特徵p的有限域.若A是一個有限維R代數,則存在R...
離散賦值環, φ(x)定義為使 的最大非負整數n,其中 表該離散賦值環的唯一極大理想。描述 在數學中,更具體地說在抽象代數和環論中,歐幾里德域(也稱為歐幾里得環)是一個可以賦予歐幾里德函式(下面解釋的)的交換環,其允許...
另外,還討論了離散賦值環、CohenMacaulay環和正則局部環。《交換代數引論》可作為本科生或研究生的交換代數和代數幾何課程的入門教材或參考書。目錄 預備知識 習題 第1章 多元多項式環與代數集 1.1 多元多項式環 1.2 代數曲線 1.3 ...
聶靈沼的數學研究工作屬代數領域,特別是在完備的離散賦值域方面。1.在域的特徵和它的剩餘域的特徵不相等的情況,在E.維特(Witt)等人工作之後,特別是對剩餘域為完滿(Perfect)時,得到一組乘性(剩餘)代表系。聶靈沼在數學學報發表...
§4.6 離散賦值域 §4.7 賦值的延拓(完備情形)§4.8 賦值的延拓(一般情形)§4.9 賦值延拓的推論 第五章 局部域及套用 §5.1 局部域上的多項式 §5.2 非分歧擴張 §5.3 完全分歧和順分歧 §5.4 慣性群與分歧群 §5.5...
除子在代數函式域 K/F 中, K 的一個不平凡賦值,若在 F 上是平凡的,則稱為 K/F 的一個賦值,由 K/F 的離散賦值所成的等價類,稱之為 K/F 的素除子。這種素除子有無限多個。作形式冪積 的積分用有限的形式表出,...
是 f 在𝓞里的代表元關於子簇Y的環𝓞的離散賦值, 是個整數,且除了有限多個Y之外, 。如果 ,其中 則韋伊除子 稱為零點除子(divisor of the zeros), 稱為函式f的極點除子(divisor of the poles)。若兩個韋伊除...
第四章 賦值與完備化 4.1p-adic數 4.2賦值 4.3數域和函式域的賦值 4.4逼近定理 4.5完備化 4.6離散賦值域 4.7賦值的延拓(完備情形)4.8賦值的延拓(一般情形)第五章 局部域及套用 第六章 類數與單位 第七章 二次域...
第四章 賦值論與完備化 4.1 p-adic數 4.2 賦值 4.3 數域和函式域的賦值 4.4 逼近定理 4.5 完備化 4.6 離散賦值域 4.7 賦值的延拓(完備情形)4.8 賦值的延拓(一般情形)4.9 賦值延拓的推論 第五章 局部域及套用 5....
曾把Julia在希爾伯特空間的兩個定理推廣至巴拿赫空間,並把吉林大學管紀文教授的文章《離散賦值完滿域的乘法群的構造》、《離散賦值完滿域上可除代數的乘法群》譯成英文,刊於1964年《中國科學》。近年任計算機教師,編制高中數學軟體。
