基本介紹
- 中文名:離散變數
- 外文名:discrete variable
- 學科:統計學
- 性質:數值只能用自然數或整數單位計算
基礎知識
基本介紹

定義
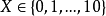
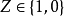


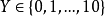

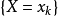



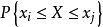
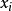

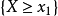

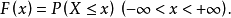


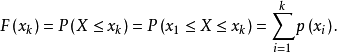
離散變數的機率分布
二項分布
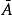
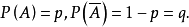
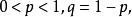

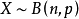
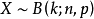
泊松分布
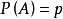

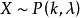



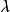
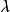
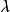
離散變數的其他分布
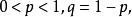
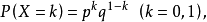
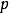
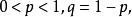





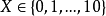
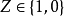


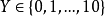

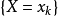



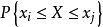
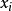

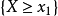

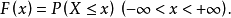


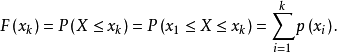
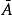
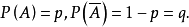
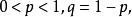

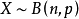
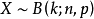
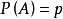

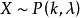



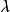
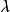
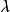
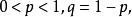
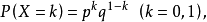
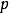
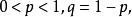



變數按其數值表現是否連續,分為連續變數和離散變數。離散變數指變數值可以按一定順序一一列舉,通常以整數位取值的變數。如職工人數、工廠數、機器台數等。有些性質...
離散數據是指其數值只能用自然數或整數單位計算的數據。例如:企業個數、職工人數、設備台數等,只能按計量單位數計數。這種數據的數值一般用計數方法取得。在統計學...
隨機變數分為離散型隨機變數與 連續型隨機變數兩種,隨機變數的函式仍為隨機變數。有些隨機變數,它全部可能取到的不相同的值是有限個或可列無限多個,也可以說機率...
離散化,把無限空間中有限的個體映射到有限的空間中去,以此提高算法的時空效率。通俗的說,離散化是在不改變數據相對大小的條件下,對數據進行相應的縮小。例如:原...
離散變f與連續變f variable dixrete and continuous符號x如果能夠表示對象集合S中的任意元素,就是變數。如果變數的域(即對象的集合5)是離散的,該變數就是離散變數...
在統計學中,變數按變數值是否連續可分為連續變數與離散變數兩種。在一定區間內可以任意取值的變數叫連續變數,其數值是連續不斷的,相鄰兩個數值可作無限分割,即可取...
離散程度,英文名Measures of Dispersion,是指通過隨機地觀測變數各個取值之間的差異程度,用來衡量風險大小的指標。...
在初等數學中,變數是表示數字的字母字元,具有任意性和未知性。把變數當作是顯式數字一樣,對其進行代數計算,可以在單個計算中解決很多問題。變數的概念也是微積分的...
離散值就是孤立的點集,像區間,它在每一點上都是連續的,而像整數集,它的每一元素之間都有一點的距離。...
變數數列是統計總體單位按一定的數量標誌分組所構成的分配數列。如,一個企業的職工,可按年齡、工齡、工資等數量標誌分組,構成變數數列。有單項式變數數列和組距式變數...
《離散變數結構最佳化設計》是2002年大連理工大學出版社出版的圖書,作者是孫煥純。...... 本書是作者20年來關於離散變數結構最佳化設計研究成果的系統歸納和總結。作者對...
相對離散指標也叫離散係數(variation coefficient)、變異係數或標準差係數等,離散係數通常是就標準差來計算的,因此,也稱為標準差係數,它是一組數據的標準差與其相應...
離散信號是在連續信號上採樣得到的信號。離散信號是一個序列,即其自變數是“離散”的。這個序列的每一個值都可以被看作是連續信號的一個採樣。...
離散選擇法(Discrete choice approach,縮寫DCA,也作Discrete choice model,即“離散選擇模型”)屬於多重變數分析的方法之一,是社會學、生物統計學、數量心理學、市場...
離散系統,廣義上指一切在時間、空間上不連續的系統;在控制理論方面,是對離散時間系統的簡稱,如果控制系統中有一處或幾處信號是一串脈衝或數碼,或者說這些信號僅...
變數值是指某一變數的具體取值。例如,參加社會保障的人數可以是604.1萬人、679.5萬人等,這些數字就是變數值。...
數理統計學:足彩離散值是機率論與數理統計,是隨機變數,是離散形隨機變數,他的值就是:分散程度的描述,指標主要是:方差和離散程度係數。但是需要指出:由於數理統計...
離散量有兩個含義,它可以指與連續量相對的、是指分散開來的、不存在中間值的量;也可以指描述數據離散趨勢的統計量,常用的表示數據離散趨勢的統計指標有全距、四...
按預先設定的算法規則,將輸入離散時間信號轉換為所要求的輸出離散時間信號的特定功能裝置。...
離散元(discrete element method, distinct element method)是一種數值計算方法,主要用來計算大量顆粒在給定條件下如何運動。...
