基本介紹
- 中文名:雅可比矩陣
- 外文名:jacobi matrix
- 定義:一階偏導數以一定方式排列成的矩陣
- 套用學科:數學
定義











例子











逆矩陣

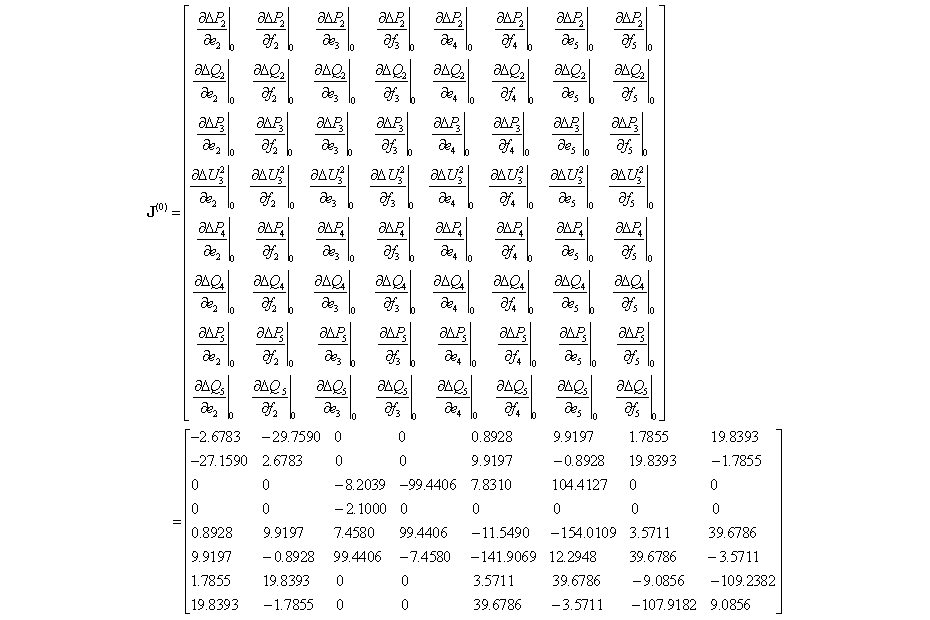
雅克比矩陣一般指本詞條























在向量微積分中,雅可比矩陣是一階偏導數以一定方式排列成的矩陣,其行列式稱為雅可比行列式。雅可比矩陣的重要性在於它體現了一個可微方程與給出點的最優線性逼近。因此,雅可比矩陣類似於多元函式的導數。定義 在向量分析中,雅可比矩陣是...
事實上,在函式都連續可微(即偏導數都連續)的前提之下,它就是函式組的微分形式下的係數矩陣(即雅可比矩陣)的行列式。 若因變數對自變數連續可微,而自變數對新變數連續可微,則因變數也對新變數連續可微。這可用行列式的乘法法則和...
之後確定疊代格式,X^(k+1) = B*X^(k) +f ,(這裡^表示的是上標,括弧內數字即疊代次數),如圖1所示,其中B稱為疊代矩陣,雅克比疊代法中一般記為J。(k = 0,1,...)再選取初始疊代向量X^(0),開始逐次疊代。收斂性...
事實上,在函式都連續可微(即偏導數都連續)的前提之下,它就是函式組的微分形式下的係數矩陣(即雅可比矩陣)的行列式。 若因變數對自變數連續可微,而自變數對新變數連續可微,則因變數也對新變數連續可微。這可用行列式的乘法法則和...
在向量微積分中,雅可比矩陣是一階偏導數以一定方式排列成的矩陣,其行列式稱為雅可比行列式。雅可比矩陣的重要性在於它體現了一個可微方程與給出點的最優線性逼近。因此,雅可比矩陣類似於多元函式的導數。
1.N a function from n equations in n variables whose value at any point is the n x n determinant of the partial derivatives of those equations evaluated at that point 雅可比行列式 [maths]短語搭配 jacobian Jacobian 矩...
附錄B量熱完全氣體數值通量雅克比矩陣推導 附錄C轉動非平衡氣體源項雅克比矩陣推導 附錄D單溫模型非平衡數值通量與源項雅克比矩陣 附錄E雙溫模型非平衡數值通量與源項雅克比矩陣 附錄F空氣化學反應模型及組分常數表 後記 彩頁 ...
設Ω 是 中的區域,n 元函式 在Ω 內可微, 稱為向量函式(vector function),亦稱為 到 的映射,記為 。它的雅可比矩陣是。 [2] 套用 編輯 向量函式的概念可直接推廣到任意維數的歐氏空間中去。像數學分析中討論實函式那樣,對...
中心流形定理(Center Manifold Theorem),控制理論中,考慮自治系統(時不變系統)dx/dt=f(x)。對其在平衡點(x*)線性化,則雅克比矩陣為A=df/dt(x*)。中心流形定理指出,如果f(x)是r階連續可導,則在任意平衡點,存在唯一的 r 階連...
其中, 是限制條件 的雅克比矩陣。(5)式意味著 的梯度應該位於限制條件梯度所張成的子空間中。對(4)和(5)套用牛頓法我們得到:其中, 是 的黑塞矩陣, 是 的的對角矩陣。因為(1)和(4),所以 在每次疊代時都必須滿足,所以可以通過...
然而該種方法也帶來了兩個缺點,其一是當強非線性時EKF違背局部線性假設,Taylor展開式中被忽略的高階項帶來大的誤差時,EKF算法可能會使濾波發散;另外,由於EKF線上性化處理時需要用雅克比(Jacobian)矩陣,其繁瑣的計算過程導致該方法...
2.1.2向量與矩陣19 2.1.3偏導數與梯度21 2.1.4雅克比矩陣22 2.1.5Hessian矩陣23 2.1.6泰勒展開24 2.1.7行列式24 2.1.8特徵值與特徵向量25 2.1.9奇異值分解26 2.1.10二次型26 2.1.11向量與矩陣求導26 2.2最...
UKF是對非線性函式的機率密度分布進行近似,用一系列確定樣本來逼近狀態的後驗機率密度,而不是對非線性函式進行近似,不需要求導計算Jacobian矩陣。UKF沒有線性化忽略高階項,因此非線性分布統計量的計算精度較高。基於上述優點,UKF被廣泛...
高斯-賽德爾疊代(Gauss–Seidel method)是數值線性代數中的一個疊代法,可用來求出線性方程組解的近似值。該方法以卡爾·弗里德里希·高斯和路德維希·賽德爾命名。 同雅可比法一樣,高斯-賽德爾疊代是基於矩陣分解原理。
其中,x y為原始數據,fun是在M檔案中定義的函式,beta0是函式中參數的初始值;beta為函式的最優值,r是各點處的擬合殘差,J為雅克比矩陣的數值。MATLAB實現 LSQNONLIN 解決非線性最小二乘法問題,包括非線性數據擬合問題;LSQCURVEFIT ...
本書對平面五桿並在線上構進行了結構分析,提出了平面五桿並在線上器人運動系統方案設計,建立了平面五桿並在線上器人的位姿正解、位姿逆解、連續軌跡逆解、運動空間分析、速度和加速度正解及逆解等數學模型,提出了構造並在線上器人雅可比矩陣的新...
14.3.3 基於圖像矩的圖像雅克比矩陣14.3.4 實際套用模型14.4 基於LMI的H控制器的設計14.4.1 模型的建立14.4.2 線性定常系統的H狀態反饋控制器的設計參考文獻 [1] 參考資料 1. Delta運算元控制及其魯棒控制理論基礎 .中國國家...
