高斯-賽德爾疊代(Gauss–Seidel method)是數值線性代數中的一個疊代法,可用來求出線性方程組解的近似值。該方法以卡爾·弗里德里希·高斯和路德維希·賽德爾命名。
同雅可比法一樣,高斯-賽德爾疊代是基於矩陣分解原理。
基本介紹
- 中文名:高斯-賽德爾疊代
- 外文名:Gauss–Seidel method
- 提出者:高斯
發展
簡介

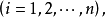
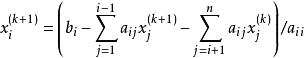
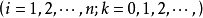


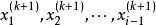
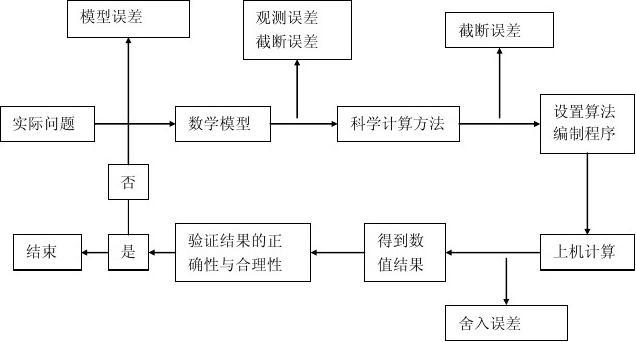
高斯-賽德爾疊代(Gauss–Seidel method)是數值線性代數中的一個疊代法,可用來求出線性方程組解的近似值。該方法以卡爾·弗里德里希·高斯和路德維希·賽德爾命名。
同雅可比法一樣,高斯-賽德爾疊代是基於矩陣分解原理。

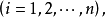
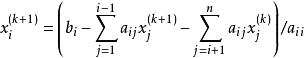
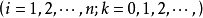


高斯-賽德爾疊代(Gauss–Seidel method)是數值線性代數中的一個疊代法,可用來求出線性方程組解的近似值。該方法以卡爾·弗里德里希·高斯和路德維希·賽德爾命名。...
中文名稱 高斯-賽德爾法 英文名稱 Gauss-Seidel method 定義 一種非線性代數方程組的疊代解法。最早用於解算電力系統潮流。這種方法具有程式編制簡單、占用記憶體少...
鬆弛法( relaxation method)是一種加速疊代方法,可視為高斯-賽德爾疊代法的推廣,對於數值計算各種問題所採用的疊代法,均可起到加速收斂的作用。此外還有超鬆弛法、...
逐次超鬆弛法(successive over relaxation method)簡稱SOR方法,解線性方程組的常用疊代法之一,它是由高斯-賽德爾疊代法經線性加速處理而得到。鬆弛方法的基礎是逐次...
在用數字計算機求解電力系統潮流問題的開始階段,人們普遍採用以節點導納矩陣為基礎的高斯-賽德爾疊代法(一下簡稱導納法)。這個方法的原理比較簡單,要求的數字計算機的...
4.4.1 雅可比疊代法 1304.4.2 高斯-賽德爾疊代法 1324.4.3 收斂性 1334.5 超鬆弛疊代法 1404.6 廣義逆 145習題4 146第5章 非線性方程(組)求根 149...
第3章解線性方程組的疊代法3.1經典疊代法的基本概念3.1.1雅可比疊代法3.1.2高斯 賽德爾疊代法3.1.3逐次超鬆弛疊代法3.2疊代法的收斂性...
4.2.1雅可比疊代法的主要思想1024.2.2雅可比疊代法的矩陣形式1034.2.3雅可比疊代法的算法和程式1044.3高斯-賽德爾疊代法1064.3.1高斯-賽德爾疊代法的主要思想106...
5.5 雅可比疊代法 5.6 高斯-賽德爾疊代法 5.7 超鬆弛疊代法 5.8 疊代法的收斂性 習題5 第6章 非線性方程的數值解法 6.1 二分法 6.2 簡單疊代...
9.3.2 雅可比疊代並行算法9.3.3 高斯-賽德爾疊代並行算法9.3.4 J疊代與G-S疊代的結合算法9.4 並行疊代算法性能分析第10章 並行計算前沿10.1 量子並行計算...
10.3.2 無回代的高斯-約旦法 237 ?10.3.3 疊代求解的高斯-賽德爾法 239 ?10.4 稀疏線性方程組的求解 241 ?10.4.1 稀疏矩陣的存儲方式 241 ?...
8.2高斯—賽德爾疊代法8.3解線性方程組的超鬆弛疊代法8.4疊代法的收斂性§9 解非線性方程組的疊代法9.1解非線性方程組的疊代法9.2解非線性方程組的牛頓法...
4.4.1雅可比疊代法 4.4.2高斯—賽德爾疊代法 4.4.3收斂性 4.5超鬆弛疊代法 4.6廣義逆 習題 第5章非線性方程(組)求根 5.1根的搜尋 5.2疊代法 ...
4.2.1 雅可比疊代法及其MATLAB程式4.2.2 高斯一賽德爾疊代法及其MATLAB程式4.2.3 逐次超鬆弛疊代法及其MATLAB程式4.2.4 三種經典疊代法的收斂條件4.3 現代變分疊代...
6.3 Gauss-Seidel(高斯-賽德爾)疊代法 6.4 鬆弛法 6.5 疊代法的收斂條件 6.6 Mathematica套用實例 習題 第7章 非線性方程(組)的數值解法 7.1 方程求根與二分...
高斯-賽德爾疊代A=[10 3 1;2 -10 3;1 3 10];b=[14 -5 14]';D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);...
熟知的簡單疊代法、高斯-賽德爾疊代法、鬆弛法等都屬此類。上兩種方法各有優缺點,直接法普遍適用,但要求計算機有較大的存儲量,疊代法要求的存儲量較小,但必須在...
2.3.2 高斯一賽德爾疊代法2.3.3 鬆弛法2.4 共軛梯度法及其基本概念2.4.1 幾個基本概念2.4.2 共軛梯度法2.5 矩陣分解2.5.1 LU分解...
附錄A疊代方法族 A.1雅可比疊代和高斯—賽德爾疊代 A.2疊代方法族 附錄B卡爾曼濾波算法與參數估計 B.1Kalman濾波器 B.2線性時變系統的卡爾曼濾波算法 ...
G-S高斯-賽德爾疊代格式 詞條標籤: 醫學術語 , 醫學 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最近更新: 創建者:科琳 猜你喜歡新手...
4.3 方程組的疊代解法4.3.1 疊代格式構造與收斂性4.3.2 雅可比疊代法(J)4.3.3 高斯一賽德爾疊代法(G—s)4.3.4 超鬆弛疊代法(SOR)...
4.6.1疊代法的基本思想4.6.2雅可比疊代法4.6.3實現雅可比疊代法的基本步驟4.6.4高斯 賽德爾疊代法4.6.5實現高斯 賽德爾疊代法的基本步驟...
3.4.2高斯-賽德爾疊代法 3.4.3鬆弛疊代法 3.4.4疊代法的收斂性及誤差估計 3.5套用實例 3.5.1用高斯消元法求矩陣的行列式和逆矩陣 3.5.2投入產出模型 3.5...
6.10高斯—賽德爾疊代法 6.11求解對稱正定方程組的共軛梯度法 6.12求解線性最小二乘問題的豪斯荷爾德變換法 6.13求解線性最小二乘問題的廣義逆法 6.14求解病...
4.3 方程組的疊代解法4.3.1 疊代格式構造與收斂性4.3.2 雅可比疊代法(J)4.3.3 高斯一賽德爾疊代法(G—s)4.3.4 超鬆弛疊代法(SOR)...
4 疊代法4.1 雅可比疊代法4.2 高斯一賽德爾疊代法4.3 疊代法收斂條件與誤差估計4.4 逐次超鬆弛疊代法5 方程組的狀態與解的疊代改善5.1 方程組的狀態與矩陣的條件...
第5章 解線性方程組的疊代法 5.1 雅可比疊代法 5.2 高斯-賽德爾疊代法 5.3 疊代法的收斂性 5.4 鬆弛疊代法 小結 習題 第6章 非線性方程的數值解法...
10.4.3 高斯一賽德爾疊代法10.4.4 超鬆弛疊代法10.4.5 多重格線法10.4.6 共軛梯度法10.5 小結和導讀習題第十一章 快速傅立葉變換...
