逐次超鬆弛法

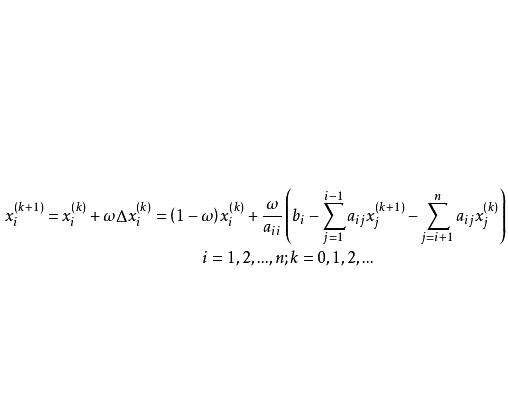
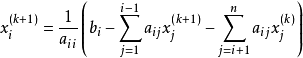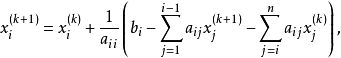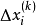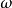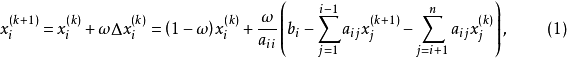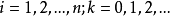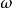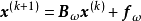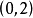逐次超鬆弛法(successive over relaxation method)簡稱SOR方法，解線性方程組的常用疊代法之一，它是由高斯-賽德爾疊代法經線性加速處理而得到。鬆弛方法的基礎是逐次減少每一個未知值的剩餘的方法，所謂剩餘是指未知值與正確解之間的差值，超鬆弛方法的基礎是使用二個逐次替換步驟進行線性外插，在這個意義上，逐次超鬆弛法可以看成是Gauss-Siedel方法(高斯-賽德爾疊代法)的推廣。

基本介紹

• 中文名：逐次超鬆弛法
• 外文名：successive over relaxation method
• 簡稱：SOR方法
• 屬性：解線性方程組的常用疊代法之一
• 所屬學科：數學

基本介紹

鬆弛法是逐步減少每個未知值偏差的一種方法。偏差是一個未知值與正確解的差。超鬆弛法是根據一種利用兩個相繼代換步驟的線性外插法。在這個意義上，逐次超鬆弛法可以看作是高斯-賽德爾法的擴充。

設方程組為

逐次超鬆弛疊代法的疊代公式為

其中ω為一參數，稱為鬆弛因子。為使疊代法收斂，理論分析表明，ω必需屬於 ，ω選取得好，可以大大加速疊代的收斂性。當係數矩陣 對角占優或對稱正定時，可保證SOR疊代法收斂。

相關分析

逐次超鬆弛法(SOR 方法，Sucessive Over Relaxation Method)可看成是Causs-Seidel方法的加速，Seidel疊代法是SOR方法的特例。

將Seidel 方法的疊代公式

改寫為

記

則

為加快收斂速度，在增量 前加一個因子 ，得

稱之為SOR 法， 稱為鬆弛因子(relaxation factor)，當 時，稱為低鬆弛法(under-relaxation method)；選擇適當的鬆弛因子能使不收斂的Gauss-Seidel疊代法變成為收斂的疊代方法，當 時，就是Gauss-Seidel疊代法；當 時，稱為超鬆弛法(over-relaxation method)，選擇適當的鬆弛因子能使收斂的Gauss-Seidel疊代法獲得加速收斂的效果。

將(1)改寫成向量形式為

由此得SOR方法的矩陣形式疊代公式為 ，其中