對稱逐次超鬆弛法(symmetric successive overrelaxation method)簡稱SSOR方法,解線性方程組的常用疊代法之一,它是逐次超鬆弛法的對稱化。
基本介紹
- 中文名:對稱逐次超鬆弛法
- 外文名:symmetric successive over relaxation method
- 簡稱:SSOR方法
- 性質:是解線性方程組的常用疊代法之一
- 所屬問題:線性方程組數值解法
- 相關問題:鬆弛法,超次鬆弛法等
基本介紹




逐次超鬆弛法

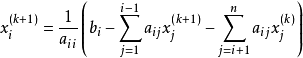
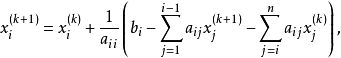


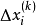
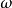
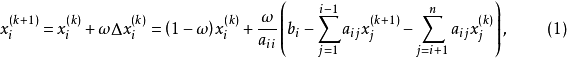
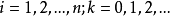
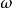




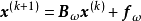


對稱逐次超鬆弛法(symmetric successive overrelaxation method)簡稱SSOR方法,解線性方程組的常用疊代法之一,它是逐次超鬆弛法的對稱化。





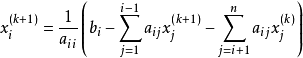
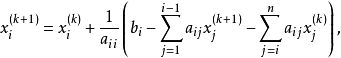


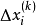
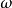
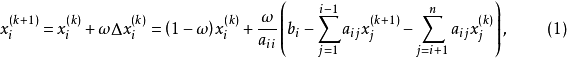
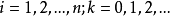




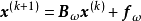

對稱逐次超鬆弛法(symmetric successive overrelaxation method)簡稱SSOR方法,解線性方程組的常用疊代法之一,它是逐次超鬆弛法的對稱化。...
逐次超鬆弛法(successive over relaxation method)簡稱SOR方法,解線性方程組的常用疊代法之一,它是由高斯-賽德爾疊代法經線性加速處理而得到。鬆弛方法的基礎是逐次...
D. M. Young於20世紀70年代提出逐次超鬆弛(Successive Over Relaxation)疊代法,簡稱SOR方法,是一種經典的疊代算法。它是為了解決大規模系統的線性等式提出來的,在...
鬆弛法( relaxation method)是一種加速疊代方法,可視為高斯-賽德爾疊代法的推廣,對於數值計算各種問題所採用的疊代法,均可起到加速收斂的作用。此外還有超鬆弛法、...
4.3.2 雅可比疊代法(J)4.3.3 高斯一賽德爾疊代法(G—s)4.3.4 超鬆弛疊代法(SOR)4.3.5 對稱逐次超鬆弛疊代(ssOR)4.4 方程組的等效最佳化解法...
4.3.5 對稱逐次超鬆弛疊代(ssOR)4.4 方程組的等效最佳化解法4.4.1 最速下降法4.4.2 共軛梯度法第5章 矩陣特徵值計算5.1 概述5.1.1 特徵值...
共扼梯度法(CG)是疊代法的主流方法之一,特別適合於特徵值為良態分布的對稱正定方程組;其它疊代法包括Jacobi、逐次超鬆弛(SOR)、廣義極小剩餘(GMRES)、預條件共...
4.2.3 反冪法及MATLAB程式 1164.3 Jacobi方法(對稱矩陣) 1184.3.1 Jacobi方法...3.4 逐次超鬆弛疊代法56小結60習題361第4章 插值與擬合634.1 引言63...
2.2.3對稱矩陣的三角分解2.2.4平方根法2.3矩陣條件數與病態方程組...3.1.2高斯 賽德爾疊代法3.1.3逐次超鬆弛疊代法3.2疊代法的收斂性...
2.4 解對稱正定矩陣方程組的平方根法3 向量與矩陣的範數3.1 向最的範數3.2 ...4.2 高斯一賽德爾疊代法4.3 疊代法收斂條件與誤差估計4.4 逐次超鬆弛疊代法...
3.5.4 利用喬列斯基分解函式解對稱正定方程組習題3第4章 線性方程組的疊代解法...4.2.2 高斯一賽德爾疊代法及其MATLAB程式4.2.3 逐次超鬆弛疊代法及其MATLAB程式...
3.4.6逐次超鬆弛疊代法 3.5矩陣特徵值問題的數值解法 3.5.1乘冪法 3.5.2反...6.5.4軸對稱問題的基本方程 6.5.5球對稱問題的基本方程 7有限單元法 7.1...
(BA)x=λx,當A、B對稱,且B正定時,可化為對稱特徵值問題(UAU)(Ux)=λ(...一類是鬆弛法,包括逐次超鬆弛法、逐次坐標超鬆弛法和共軛梯度法等;另一類是變換...
1.5.3 Hermite矩陣和實對稱矩陣的特徵值和特徵向量習題1.51.6 實二次型習題1.6...2.3 直接法的誤差分析2.4 線性方程組的疊代解法2.5 逐次超鬆弛疊代法和塊疊代...
5.3.3 Gauss-Seidel疊代法 178 5.3.4 逐次超鬆弛疊代法 180 5.3.5 梯度...10.2.3 反冪法 350 10.2.4 混合冪法 352 10.3 實對稱矩陣的Jacobi法 ...
5.5.3 逐次超鬆弛疊代法 1465.6 實驗範例:正方形槽的電位分布 1495.7 上機...10.2.1 實對稱矩陣的旋轉正交相似變換 31110.2.2 jacobi方法 313...
3.3.2 對稱正定矩陣的平方根法 3.3.3 解三對角...4.1.3 超鬆弛疊代法 4.2 疊代法的收斂性 4.2.1 ...8.3.3 區間逐次分半求積法 8.4 龍貝格求積方法 8.5...
1.5.3 Hermite矩陣和實對稱矩陣的特徵值與特徵向量(38) 習題1.5(42) 1.6 ...2.5.1 逐次超鬆弛疊代法(188) 2.5.2 塊疊代法(191) 2.6 疊代法的數值...
2.2 杜利特爾分解法2.3 解三對角線方程組的追趕法2.4 解對稱正定矩陣方程組...4.2 高斯一賽德爾疊代法4.3 疊代法收斂條件與誤差估計4.4 逐次超鬆弛疊代法...
