基本介紹
- 中文名:隨機擴散
- 外文名:Random diffusion
- 描述:任意方向擴散運動
- 套用:氣相色譜
- 學科:生物
概念
基於分離粒子隨機擴散理論
模擬與計算方法
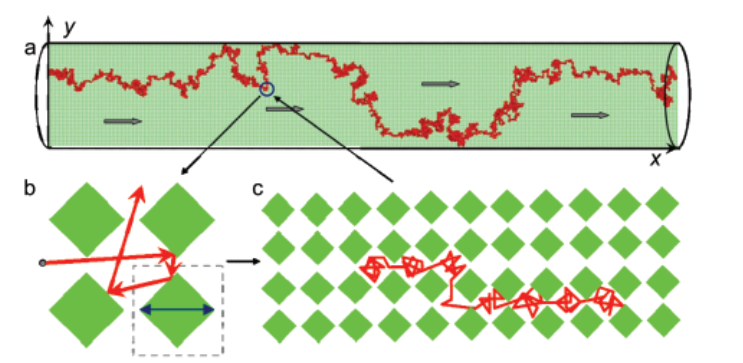
分離柱
分離物
擴散過程
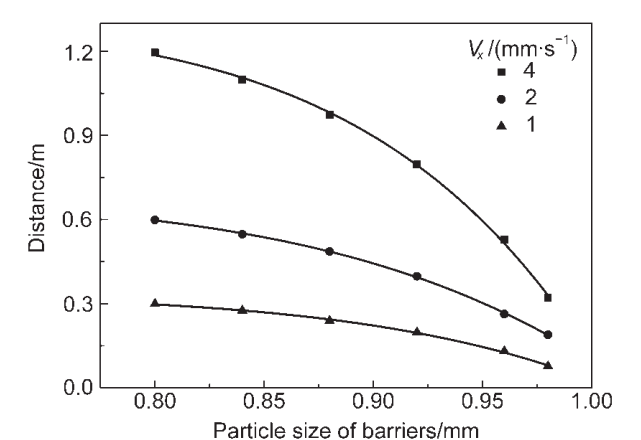
固定相的填充率
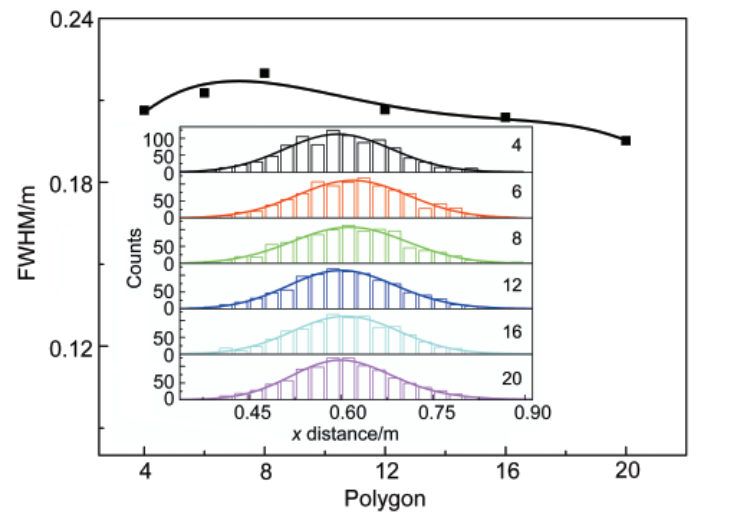
固定相的形狀
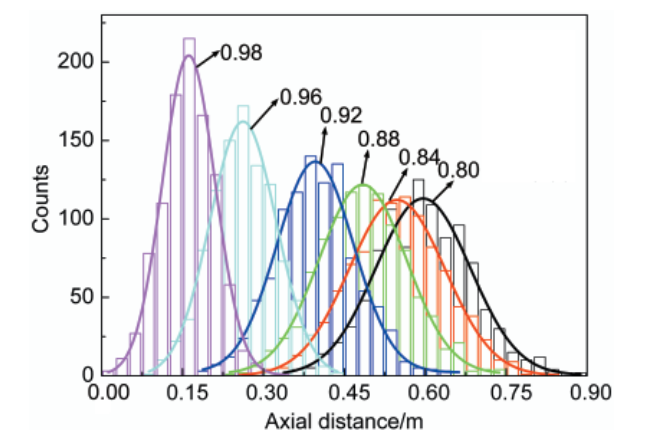
柱長
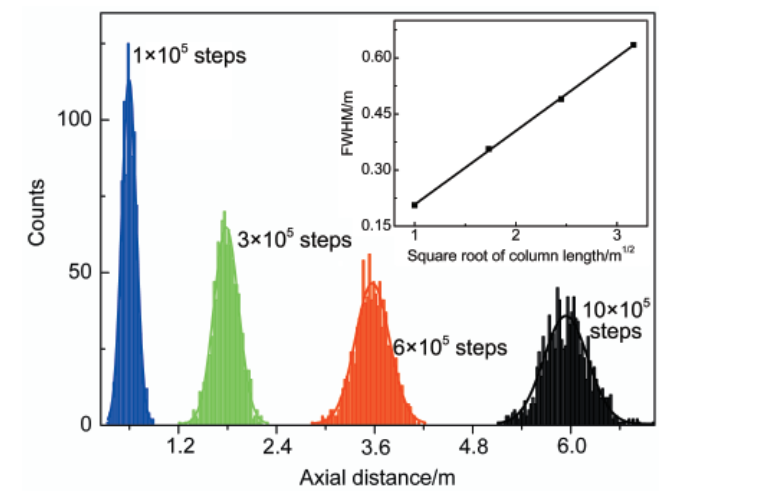





隨機擴散是指物質通過不同的方式進行擴散,有些需要能量,有些需要載體。自由擴散在生物中指的是不需要載體和能量的順濃度梯度的被動運輸方式。兩者的區別是,自由擴散有指定運輸方向(順濃度),而隨機擴散是任意方向。概念隨機擴散是指...
大氣擴散方程 大氣擴散方程是2009年公布的大氣科學名詞。定義 擴散物質在湍流運動中質量守恆定律的表達式。例如用大氣擴散K理論導出的平流擴散方程及高斯擴散模式等。出處 《大氣科學名詞》。
隨機環境中的隨機遊動 [random walk in random environments]設(V,E)是無窮的有向圖,具有可數的頂點集 V 和邊集 。對任意 ,定義它的鄰域(neighborhood),表示支撐為 的 V 上的機率測度全體。中的元素稱為在 v 點的轉移律(...
隨機遊走(random walk)也稱隨機漫步,隨機行走等是指基於過去的表現,無法預測將來的發展步驟和方向。核心概念是指任何無規則行走者所帶的守恆量都各自對應著一個擴散運輸定律,接近於布朗運動,是布朗運動理想的數學狀態,現階段主要套用...
蒙特卡洛擴散模擬又稱隨機遊走擴散模擬,是利用計算機產生大量粒子的隨機遊走軌道模擬湍流擴散。一般作法是想像式地釋放成千上萬個粒子模擬污染物質,各個粒子每次都以一個夠短的時間長作隨機遊走,最終形成大量的隨機軌道。由穿過單位體積的...
種子散落屬於被動擴散;有些小昆蟲飛翔力不強,方向和距離也基本是隨機的,所以也表現上述規律。擴散是研究種群數量變動的重要因子。在生產實踐中,害蟲和雜草的擴散會給人類健康和農牧業帶來損害。因此,了解生物擴散的特性,對防治有害生物有...
生物種群模型的正穩態解一直是數學家的重要研究課題之一,本項目主要致力於空間非均勻性與交錯擴散對正穩態解的影響。為此,主要考慮了不同非均勻空間中的隨機擴散捕食模型與均勻空間中的交錯擴散捕食或食物鏈模型的正穩態解的性質。通過...
《同胚群上的擴散過程與多值隨機微分方程》是依託中山大學,由任佳剛擔任項目負責人的面上項目。 中文摘要 本項目將研究圓環面之微分同胚群上的擴散過程的存在性與正則性,即:在高維情形證明存在取值於圓環面之同胚群的Brown運動,在一維...
分數階微積分具有非局部性及記憶性,從而非常適合用於描述自然界中的反常擴散現象。從現實問題中,抽象出分數階反常擴散方程後,如何求解這類問題,是當前一個熱門問題。本項目結合分數階微積分運算元的性質,從隨機遊走模型出發,引入隨機表示...
《一類與擴散過程相關的半無界問題的隨機解》是依託華南師範大學,由陳曉珊擔任項目負責人的數學天元基金項目。項目摘要 擴散模型在金融數學中,特別是期權定價中有著非常重要的作用。本項目主要以隨機分析的理論為工具來研究一個指定資產的...
《創新擴散的隨機理論與實證研究》是依託北京航空航天大學,由官建成擔任項目負責人的面上項目。項目摘要 以治理產品質量差、經濟效益低為內容,從技術、管理、巨觀、微觀等方面找出質量差、效益低的根本原因,提出解決的主要對策。研究成果...
《擴散過程及其樣本軌道》是2010年世界圖書出版公司出版的圖書,作者是伊藤清。內容介紹 《擴散過程及其樣本軌道(英文版)》是Springer《數學經典教材》系列之一,對與擴散現象有關的隨機過程產生持久而深刻的影響。不少數學家受益於《擴散...
《隨機偏微分方程和互動擴散過程遍歷理論中的一些問題》是依託北京大學,由劉勇擔任項目負責人的面上項目。項目摘要 具有周期性和多孔性的點陣材料與結構,是極具套用潛力的輕質高強多功能材料,在國內外航空航天、艦船/潛艇等諸多高科技...
《超光速電磁波對高能電子隨機加速和投擲角擴散的研究》是依託長沙理工大學,由肖伏良擔任項目負責人的面上項目。項目摘要 理論分析和觀測數據均表明:磁暴時地球輻射帶高緯區域超光速(相速度大於光速)電磁波幅度增強,高能電子沉降過程加劇;...
《擴散過程離散化形式下的若干統計問題的大偏差原理》是依託河南師範大學,由苗雨擔任項目負責人的面上項目。項目摘要 擴散過程是隨機微分方程中最為重要的模型之一,有著廣闊的套用背景,特別 是在金融數學領域。有關擴散過程的統計推斷...
由於 過程 統計的需要,這一問題在以後引起了相當大的重視和大量的工作,對於各類重要的 過程,如正態 過程(見 隨機過程)、 獨立增量過程、擴散 過程(見 馬爾可夫過程)、 點過程乃至一般的半鞅(見 鞅),都先後討論了這一問題。在...
其主要原因不僅是每個基因是自我繁殖的實體,而且它的頻率幾乎是隨時間連續變化的.因為在漫長的進化過程中,基因頻率的變化即使以世代為時間單位,也是非常緩慢的.於是,完全可以把基因頻率的變化過程看成是連續的隨機過程,進而假設基因頻率...
《擴散的小球》是一款益智小遊戲,遊戲大小為28.77KB。遊戲介紹 紅藍兩種顏色的小球在各自的空間做著隨機的擴散運動,你需要利用中間擋板上的小口將兩種小球引到對應的空間之中,快來試試看吧。遊戲畫面精緻,遊戲非常具有挑戰性,適合...
模型的錯誤設定可能導致金融決策的重大失誤,因而擴散型模型設定檢驗問題的研究是非常必要的。本課題對包括一維擴散,時變擴散,隨機波動率模型的擴散型模型設定檢驗問題展開深入研究。首先通過用CK方程數值解逼近設定模型轉移密度並用平面擬合...
能量擴散的作用:如果發射信號的能量過於集中在某些局部頻譜段上,將對與其共用頻段的其他系統或設備,如:相鄰的衛星、同一衛星的其它轉發器、同一轉發器的其它載波以及同頻段的地面微波系統造成較大幹擾。通過人為地對發射信號進行隨機化或...
分子擴散是在一相內部有濃度差異的條件下,由於分子的無規則隨機熱運動而產生的物質傳遞現象。分子擴散是分子微觀運動的結果。儘管分子運動的速度較大,但由於分子運動的途徑是隨機的,它沿一個方向運動很短距離就可能與另外的分子碰撞,而...
如果進一步仔細觀察它的路徑,就會發現,這非常近似於數學上隨機漫步(random walk)。這種路徑由愛因斯坦在對布朗運動的研究中進行了著名的分析,他發現:做隨機漫步的粒子的移動距離的平方的平均數與時間成正比。這個關係式可以表示為: = ...
速率理論認為,單個組分分子在色譜柱內固定相和流動相間要發生千萬次轉移,加上分子擴散和運動途徑等因素,它在柱內的運動是高度不規則的,是隨機的,在柱中隨流動相前進的速率是不均一的。與偶然誤差造成的無限多次測定的結果呈正態...
