基本介紹
- 中文名:隨機信號分析
- 外文名:Random Signal Analysis
- 套用學科:通信
機率論基礎知識
隨機試驗
隨機事件
樣本空間
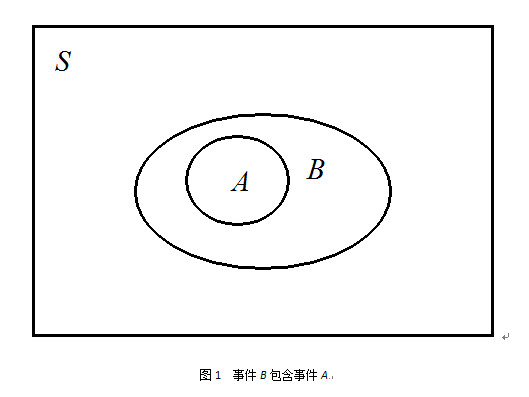



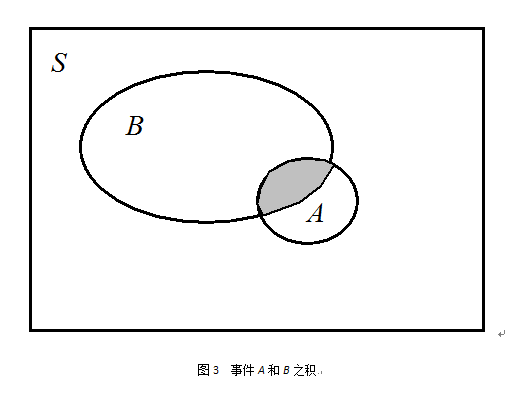


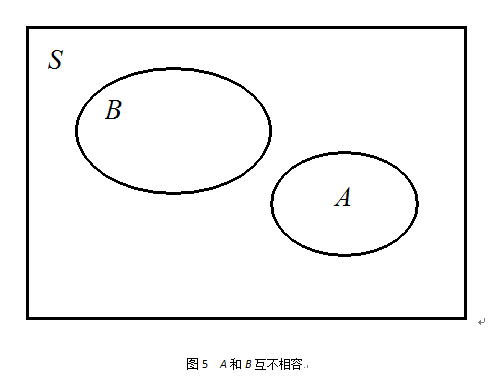




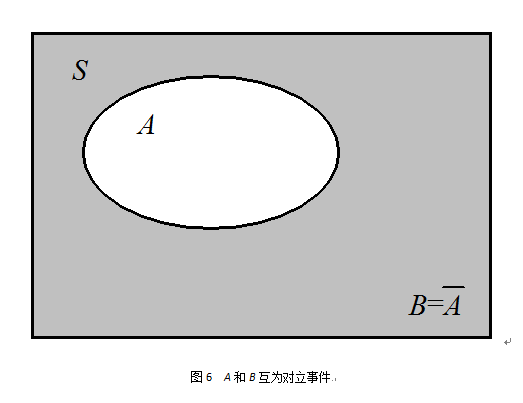
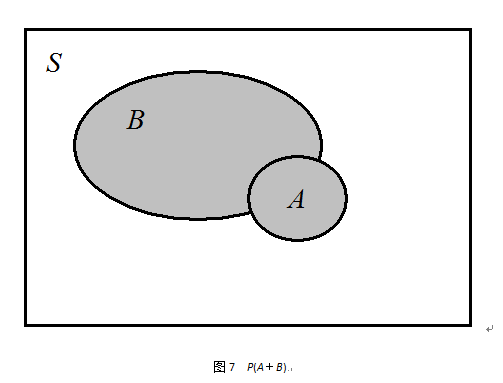
機率









隨機變數

隨機過程






























《隨機信號分析》共分為5章。主要內容包括:隨機變數基礎知識;隨機信號的基本概念,涉及平穩、遍歷隨機信號的基本內容;平穩隨機信號的譜分析;線性系統對隨機信號的作用...
隨機信號分析(第4版)主要討論隨機信號的基礎理論和分析方法。全書共7章,內容包括:機率論基礎,隨機信號與典型信號舉例,平穩性、循環平穩性與功率譜密度函式,各態歷...
隨機信號分析(第2版)詳細介紹了電子系統中常用隨機信號的統計特性,包括白噪聲、高斯過程、窄帶過程、馬爾可夫過程,並介紹了現代信號處理中常用的隱馬爾可夫的概念,以及...
《隨機信號分析與處理》是2006年6月1日清華大學出版的圖書,作者是羅鵬飛、 張文明。本書主要是把隨機信號分析、信號檢測與估計的內容有機地融合在一起的電子信息...
信號可按其發生的規律分為確定信號和隨機信號。隨機信號在通信系統中大量存在。首先,通信系統中傳送的訊息本身就是隨機的。傳送端將要傳送什麼樣的訊息,對於收信者...
《隨機信號分析與處理(第2版)》是2014年清華大學出版社出版的圖書,作者是羅鵬飛、張文明。...
《隨機信號分析教程》從人們對於隨機現象認識的角度出發,注重機率論與隨機過程之間的聯繫和區別,對隨機過程的定義、描述方法和特性作了詳細介紹。從系統的角度,對隨機...
《隨機信號分析基礎》是2009年03月電子工業出版社出版的圖書,作者是王永德。該書為普通高等教育“十一五”國家級規劃教材。主要從工程套用的角度討論隨機信號(隨機...
《隨機信號分析及套用》是2011年3月1日清華大學出版社出版的圖書,作者是潘建壽。本書介紹了幾種常用的隨機過程,可作為普通高校電子信息類、通信類、電子類等專業的...
《隨機信號分析與套用》是2013年出版的圖書,作者是劉磊、王琳。本書主要討論隨機信號的基礎理論和分析方法。全書共分6章,包括機率論基礎,隨機信號的時、頻域特性,...
內容簡介 《隨機信號分析與套用》主要從工程套用的角度討論隨機信號(隨機過程)的理論分析和實驗研究方法。《隨機信號分析與套用》共五章,內容包括:隨機過程;隨機過程...
《隨機信號分析與最優估計理論》是2012年國防科技大學出版社出版的圖書,作者是潘仲明。《隨機信號分析與最優估計理論》適合作為高等學校儀器儀表、機械工程、電氣工程...
《隨機信號分析與處理簡明教程》是2009年0電子工業出版社出版的圖書,作者是羅鵬飛。...
《隨機信號分析解題指南》是2007年北京理工大學出版社出版的圖書,作者是李永慶。...... 《隨機信號分析解題指南》是2007年北京理工大學出版社出版的圖書,作者是李永慶...
《隨機信號分析的工程套用》是2009年國防工業出版社出版的圖書,作者是張強。...... 《隨機信號分析的工程套用》是2009年國防工業出版社出版的圖書,作者是張強。...
《非平穩隨機信號分析與處理》是2008年國防工業出版社出版的圖書,作者是王宏禹、陳喆。...
《隨機信號處理原理與實踐》是2010年6月1日科學出版社出版的圖書,作者是楊鑒。...... 全書共8章,內容包括離散時間信號處理基礎、隨機信號分析基礎、隨機信號的線性...
確定性信號是指可以用明確的數學關係或者圖表描述的信號。若信號被表示為一確定...1. 郭業才,阮懷林.隨機信號分析:合肥工業大學出版社,2009.8 詞條標籤: 科學百科...
腦電信號分析方法近年來得到很快發展 ,並且開始套用於臨床 ,進一步提高了診斷效果。...
內容簡介本書為普通高等教育“十一五”、“十二五”國家級規劃教材,是四川省精品課程“隨機信號與系統”的主講教材。本書主要討論隨機信號的基礎理論和分析方法。全書...
《通信信號分析與處理》是2009年09月合肥工業大學出版社出版的圖書,作者是郭業才。《通信信號分析與處理》以通信信號的傳送、傳輸與接收為主線,介紹了通信中的隨機...
內容包括:通信與信息工程領域所涉及到的隨機現象和隨機問題;機率論和隨機過程基礎;常見隨機過程的機率模型及其性質;隨機信號分析的基礎知識,如隨機信號的正交分解、...
圖書簡介本書詳細介紹信息傳輸系統方面的內容,包括信號、系統與噪聲的基本理論和各種通信系統的基本原理。全書共分5章,第1章確定信號分析,第2章隨機信號分析,第3章...
《信號分析與處理》是一本正文語種為簡體中文的書籍。...... 復頻域)、離散信號分析(時域、頻域、復頻域)、信號處理基礎、模擬和數字濾波器、隨機信號分析與處理基...
《信號檢測與估計》是張立毅編著的圖書,共分12章,系統地介紹了信號檢測與估計的基本理論。首先闡述了本課程的基礎理論、隨機信號分析及其統計描述。其次,介紹了經典...
李曉峰,在無線通信與DSP實時實現技術、移動多媒體傳輸與網路服務、圖像和語音信號處理等方向有較深入研究。獲得國家、省/部級科技獎6項;講授《通信原理》、《隨機...
