隨機信號(random signal),幅度未可預知但又服從一定統計特性的信號,又稱不確定信號。
基本介紹
- 中文名:隨機信號
- 外文名:random signal
- 別名:不確定信號
- 頻域:連續的
- 特點:不能預測其未來任何瞬時值
- 套用學科:通信
定義
隨機信號的分類
統計特性
隨機過程
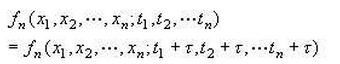 圖1
圖1隨機信號(random signal),幅度未可預知但又服從一定統計特性的信號,又稱不確定信號。
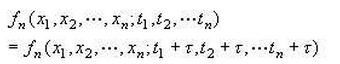 圖1
圖1隨機信號(random signal),幅度未可預知但又服從一定統計特性的信號,又稱不確定信號。...
信號可按其發生的規律分為確定信號和隨機信號。隨機信號在通信系統中大量存在。首先,通信系統中傳送的訊息本身就是隨機的。傳送端將要傳送什麼樣的訊息,對於收信者...
偽隨機信號,又稱偽隨機序列或偽隨機碼,是由周期性數字序列經過濾波等處理後得出的,它具有類似於隨機噪聲的某些統計特性,同時又能夠重複產生。常見的偽隨機信號主要...
《隨機信號分析》共分為5章。主要內容包括:隨機變數基礎知識;隨機信號的基本概念,涉及平穩、遍歷隨機信號的基本內容;平穩隨機信號的譜分析;線性系統對隨機信號的作用...
隨機信號分析(第4版)主要討論隨機信號的基礎理論和分析方法。全書共7章,內容包括:機率論基礎,隨機信號與典型信號舉例,平穩性、循環平穩性與功率譜密度函式,各態歷...
《隨機信號處理》是2009年08月合肥工業大學出版社出版的圖書,作者是郭業才。...... 《隨機信號處理》每章都有相應的MATLAB仿真實例與習題,內容組織體現了“重視基礎...
《隨機信號與系統》主要討論隨機信號的基礎理論和分析方法。全書共分5章,包括機率論基礎,隨機信號的時、頻域特性,隨機信號通過線性系統的特性,隨機信號的相關實驗與...
《隨機信號分析與處理》是2006年6月1日清華大學出版的圖書,作者是羅鵬飛、 張文明。本書主要是把隨機信號分析、信號檢測與估計的內容有機地融合在一起的電子信息...
確定性信號是指可以用明確的數學關係或者圖表描述的信號。若信號被表示為一確定的時間函式,對於指定的某一時刻,可以確定一相應的函式值,這種信號被稱為確定性信號。...
隨機信號分析(第2版)詳細介紹了電子系統中常用隨機信號的統計特性,包括白噪聲、高斯過程、窄帶過程、馬爾可夫過程,並介紹了現代信號處理中常用的隱馬爾可夫的概念,以及...
《隨機信號分析與處理(第2版)》是2014年清華大學出版社出版的圖書,作者是羅鵬飛、張文明。...
平穩信號分嚴平穩和寬平穩,嚴平穩的條件在信號處理中太嚴格,不實用,一般所說的平穩是指寬平穩。...
《隨機信號分析基礎》是2009年03月電子工業出版社出版的圖書,作者是王永德。該書為普通高等教育“十一五”國家級規劃教材。主要從工程套用的角度討論隨機信號(隨機...
非平穩信號是指分布參數或者分布律隨時間發生變化的信號。平穩和非平穩都是針對隨機信號說的,一般的分析方法有時域分析、頻域分析、時頻聯合分析。非平穩隨機信號的...
《隨機信號分析與套用》是2013年出版的圖書,作者是劉磊、王琳。本書主要討論隨機信號的基礎理論和分析方法。全書共分6章,包括機率論基礎,隨機信號的時、頻域特性,...
《隨機信號分析教程》從人們對於隨機現象認識的角度出發,注重機率論與隨機過程之間的聯繫和區別,對隨機過程的定義、描述方法和特性作了詳細介紹。從系統的角度,對隨機...
《隨機信號分析及套用》是2011年3月1日清華大學出版社出版的圖書,作者是潘建壽。本書介紹了幾種常用的隨機過程,可作為普通高校電子信息類、通信類、電子類等專業的...
《隨機信號估計與系統控制》是北京工業大學出版社2001年出版的圖書,作者是徐寧壽。...... 《隨機信號估計與系統控制》是北京工業大學出版社2001年出版的圖書,作者是...
《隨機信號與系統》是2013年出版的圖書,作者是潘仲明。...... 隨機信號與系統內容簡介 編輯 本書詳盡介紹了隨機過程、最優估計、時間序列模型和線性動態系統辨識、譜...
內容簡介本書為普通高等教育“十一五”、“十二五”國家級規劃教材,是四川省精品課程“隨機信號與系統”的主講教材。本書主要討論隨機信號的基礎理論和分析方法。全書...
全書共10章,內容包括:隨機信號兩種統計特性的描述方法,重點介紹數字特徵,如均值、方差、相關函式、相干函式、功率譜密度、高價譜、譜相關理論和機率密度函式等的表述...
《隨機信號處理教程》是2010年北京郵電大學出版社出版的圖書,作者是印勇。...... 《隨機信號處理教程》從信號分析與處理的角度組織內容的編寫,結合信號分析與處理的...
《隨機信號分析的工程套用》是2009年國防工業出版社出版的圖書,作者是張強。...... 《隨機信號分析的工程套用》是2009年國防工業出版社出版的圖書,作者是張強。...
《非平穩隨機信號分析與處理》是2008年國防工業出版社出版的圖書,作者是王宏禹、陳喆。...
簡介離散隨機信號處理discrete random signal processing利用數字運算,對離散隨機信號進行各種濾波處理、離散變換和譜分析。隨機信號是一種非確定性的信號,如熱噪聲信號...
《信號分析》是2001年6月科學出版社出版的圖書,作者是臼井支朗、盧乃洪,譯者是何希才。...
《隨機信號處理原理與實踐》是2010年6月1日科學出版社出版的圖書,作者是楊鑒。...... 《隨機信號處理原理與實踐》系統地介紹了隨機信號處理的基本理論、算法及套用...
平穩信號是指分布參數或者分布律隨時間不發生變化的信號。...... 針對隨機信號 平穩和非平穩信號都 注意 平穩信號的均值和時間無關, 平穩信號的統計特性不隨時間變...
