基本介紹
- 中文名：阿廷映射
- 外文名：Artin mapping
- 領域：數學
- 學科：類域論
- 定義：理想群到伽羅瓦群的映射
- 意義：類域論的基石之一
- 釋義：理想群(或伊代爾群)到伽羅瓦群的映射
概念,映射,伊代爾群,伽羅瓦群,類域論,
概念
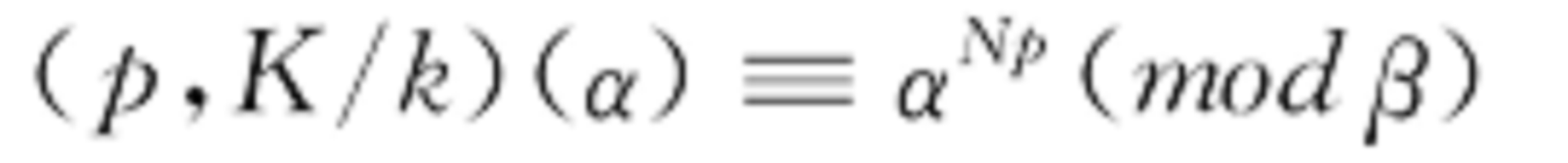
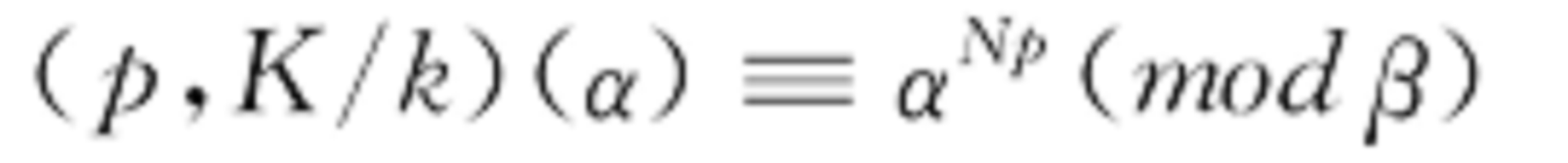
阿廷映射(Artin mapping)是理想群(或伊代爾群)到伽羅瓦群的映射。它是類域論的基石之一。設K/k為數域的伽羅瓦擴張，p是k的素理想，β是p在K的素理想因子。伽羅瓦群G(K/k)中保持β不變的元素記為Gβ。剩餘類域K'=K(mod β)是k'的f次循環擴張，伽羅瓦群記為G'，生成元為σ'。Gβ到有自然滿同態，核為Tβ。當K/k為阿貝爾擴張且p在K非分歧時，Tβ=1。Gβ在Gβ中的原像是G(K/k)中一個元素且僅與p有關，記為(p，K/k)。由p→(p，K/k)按乘法拓展可得到由k的與K/k判別式互素的理想群I(d)到G(K/k)的映射A。此映射稱為阿廷映射，(p，K/k)稱為阿廷符號。阿廷映射是滿射，因此，在確定其核kerA之後，就有同構：I(d)/kerA≌G(K/k)。
這是類域論基本定理的原型。進而，可以定義廣義理想群及伊代爾群上的阿廷映射。上述阿廷映射及阿廷符號(p，K/k)由下式惟一確定：
(對K的任一整數α成立)，式中Np為k'的元素個數。
映射
映射亦稱函式。數學的基本概念之一.也是一種特殊的關係。設G是從X到Y的關係，G的定義域D(G)為X，且對任何x∈X都有惟一的y∈Y滿足G(x，y)，則稱G為從X到Y的映射。即關係G為映射時，應滿足下列兩個條件：
1.(x∈X)(y∈Y)(xGy).
2.(x∈X)(y∈Y)(z∈Y)((xGy∧xGz)→y=z).這個被x∈X所惟一確定的y∈Y，通常表示為y=f(x)(x∈X).f(x)滿足：
1) f(x)∈Y.
2) G(x，f(x))成立(x∈X).
3)z∈Y，G(x，z)→z=f(x).
關係G常使用另一些記號：f：X→Y或XY。f與G的關係是y=f(x)(x∈X)，若且唯若G(x，y)成立.可取變域X中的不同元素為值的變元稱為自變元或自變數。同樣可取變域Y中的不同元素為值的變元稱為因變元或因變數。始集X稱為映射f的定義域。記為D(f)或dom(f).終集Y稱為映射的陪域，記為C(f)或codom(f)。Y中與X中的元素有關係G的元素的組合{y|x(x∈X∧y=f(x)∈Y)}稱為映射的值域，記為R(f)或ran(f)。當y=f(x)時，y稱為x的象，而x稱為y的原象。y的所有原象所成之集用f(y)表示。對於AX，所有A中元素的象的集合{y|x(x∈A∧y=f(x)∈Y)}或{f(x)|x∈A}稱為A的象。記為f(A).對於BY，所有B中元素的原象的集合{x|x∈X∧y(y∈B∧y=f(x))}稱為B的原象。記為f(B)。顯然f(A)=f(x)，f(B)=f(y)。
伊代爾群
伊代爾群是一種特殊的群。即各分量為諸局部域元素的某些向量(其分量幾乎均為單位)形成的群，是理想群和除子群的推廣。設F為整體域，M為其素除子集，FP為F對P∈M的完備化。設a=(aP)為積空間ΠFP(P∈M)中元素，若對幾乎所有P∈M(即除有限個之外對所有的有限素除子P∈M)均有aP為FP的單位，則a=(aP)為F的伊代爾.F的伊代爾全體J形成群(按分量進行乘法)，稱為伊代爾群。F按對角線嵌入J，稱為主伊代爾群.自1936年由謝瓦萊(Chevalley，C.)引入以來，伊代爾群在數論中套用很廣泛。伊代爾群與理想群關係密切。事實上，J/FJ∞與F的理想類群H同構，式中J∞表示對有限素除子P∈M均有aP為單位的伊代爾(aP)全體。伊代爾群是一個局部緊的拓撲群。
伽羅瓦群
伽羅瓦群是伽羅瓦理論的一個重要概念。設K是域F的伽羅瓦擴域，K的F自同構群G(K/F)稱為K/F的伽羅瓦群。當K為F可分閉包時，G(K/F)稱為F的絕對伽羅瓦群。若K是F的一個有限次伽羅瓦擴域，則G(K/F)是一個[K∶F]階群。由於有限次伽羅瓦擴域等同於某一可分多項式的分裂域，因此，若域K是域F上一個可分多項式f(x)的分裂域，則其伽羅瓦群G(K/F)就稱為f(x)的伽羅瓦群，從而有限次伽羅瓦擴域的伽羅瓦群必為某一多項式的伽羅瓦群。在歷史上，是伽羅瓦(Galois，E.)首先對多項式引入伽羅瓦群的概念。
類域論
類域論是代數數論的重要理論之一。它深刻地刻畫了(相對)阿貝爾擴張。基本定理如下：若K/k為數域的有限阿貝爾擴張，伽羅瓦群為G=G(K/k)，則存在k的模f(稱為K/k的導子，是k的一個除子)，使得對k的任意的模m，由f|m得出G同構於m射線類群I(m)/PmN(m)，式中I(m)為與m互素的k的理想集，N(m)為與m互素的K的理想到k的范全體，Pm為模m餘1的α∈k生成的主理想集。且k的素除子v在K分歧若且唯若v|f；k的與m互素的素理想p在K完全分裂若且唯若p∈PmN(m).反之，對k的任一模m及I(m)的任一含Pm子群H，總存在惟一阿貝爾擴張K/k，使得H=kPmN(m)且上述事實均成立。特別地，G(K/k)I(m)/H。更經常的是用伊代爾語言敘述類域論的定理。基本定理：若K/k為數域的有限阿貝爾擴張，則伽羅瓦群G(K/k)同構於Jk/kNJk，式中Jk為k的伊代爾群，NJK為K的伊代爾群到k的范。上述群的同構由阿廷映射給出。由此可得出，數域k的諸有限阿貝爾擴張K/k與Jk的含k諸開子群H之間一一對應，即K對應於H=kNJK，稱為H的類域，G(K/k)Jk/H；這一對應是這兩個格(對於複合(或積及交))的反向(包含關係)格同構。類域論有系統的定理和套用，有多種不同的表述方式。對於局部域的阿貝爾擴張有類似的定理(局部類域論)，對於有限域上的單變數函式域也有類似的定理。
