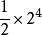基本介紹
部分實施法指在析因試驗的全部因子水平組合(處理方法)中,只挑選一部分有代表性的水平組合實施試驗的方法。其優點是工作量小且結果容易控制;其缺點是試驗誤差較全面試驗要大而估計量的精確度較小(至少理論上如此),且試驗結果的解釋較複雜。
析因試驗設計是任意r(r≥1)個因子,每個因子取任意給定數目
水平的試驗的設計;分為全面析因試驗設計和部分實施析因試驗設計兩大類,其中因子的水平是可以控制的或者隨機選取的。每個因子各取一個水平,r個水平構成一個水平組合,總共有
個不同的的水平組合(亦稱試驗點或處理方法)。對每一水平組合至少進行一次試驗(對—個單元進行試驗)的設計叫做全面設計,其優點是能考察全部主因子效應和全部互動效應,其缺點是工作最大甚至無法實施,結果也難以控制。1946年芬尼(D.J.Finney)提出了部分實驗法,即只挑選一部分有代表性的水平組合進行試驗的方法,其實質是忽略全部或大部不顯著互動效應(如,忽略全部三階及三階以上互動效應),
正交拉丁方和
正交表就是部分實施的重要工具。
相關說明與舉例
在有若干個因素的因子配置試驗里,需要測定的次數將大為增加。而且所得到的多數資料被用於估計高次互相作用的目的,或者用於不需要十分精確的誤差分析。因此,如果有5種因素或變數,分別具有兩個水平的情況下,一個完整的試驗就需要32次觀測。這就能得出6個主要效果,一次互相作用10個,兩次互相作用是10個,三次互相作用是5個,四次互相作用只有(ABCDE)1個。如果在估測時認為這些作用的任何一個都可以忽略時,則習慣上把它們看做誤差的來源而被用於誤差分析。
在許多情況下,與其認為高次互相作用對於保證實驗精確度的良好分析值是必要的,倒不如事先假定許多高次互相作用是可以忽視的,這樣則更為合理。特別是在因素中有幾個大致顯示出是獨立變數時更是如此。如果這類的變數確實是獨立的,甚至連主效應也沒有的話,那么,它們的高次互相作用大概更可以忽略。通過如此處理,有時對高次互相作用作某些犧牲就能夠使觀測次數減少。這種方法就是人們已知的部分實施法。
現在讓我們來看一下一個最簡單的例子,3個因素A、B、C各有兩個水平時的情況。此時完整的試驗構成下面圖(1)的型式。
 圖1
圖1效果表現為表1的形式,其中把構成左邊表示的互相作用的觀測值符號列在各自的下面。 ·
| abc | ab | ac | bc | a | b | c | 1 |
A | + | + | + | - | + | - | - | - |
B | + | + | - | + | - | + | - | - |
C | + | - | + | + | - | - | + | - |
AB | + | + | - | - | - | - | + | + |
AC | + | - | + | - | - | + | - | + |
BC | + | - | - | + | + | - | - | + |
ABC | + | - | - | - | + | + | + | - |
那么,現在假設去掉一半觀測,特別是不做abc、a、b,c。此時,若再假設使用和上表同樣的符號來構造剩餘觀測的1次組合。由於A和-BC現在已經不存在把二者區分開來的一項,所以就已經不能區分了。同樣,B和-AC,C和-AB,-ABC,及總平均也不再能單獨計算。因而在這種減半實施的試驗里,如果可以假定BC、AC,AB的互相作用能夠忽略,則可分析主要的影響。也就是說,只要進行ab、ac、bc、1的4個觀測,就足以分析總平均值和三個主要影響,這時假定不存在相互作用,但是這4個觀測既不提供任何檢驗這一假定的方法, 也不能給出分析誤差的方法。
如果減半實施的個數較多,也就能得到大量的數據。若4種因素處在兩個水平,則有
即8個觀測值。在可以忽略高次相互作用時,它們可用於給出4個主要影響和3個1次相互作用。假如相互作用確實能夠全部忽略,則這些式中的3個就可以用於求得誤差的極限值。
其他比例——譬如1/4,也是可能的。它們通常僅僅在因子個數非常多的時候才使用。
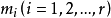
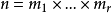
 圖1
圖1