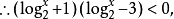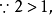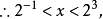超越不等式

超越不等式(transcendental inequality)是一種特殊不等式，指含超越式的不等式，例如sin x-cos y≤1，log₃(x²-2x)>0等，除指數不等式、對數不等式、三角不等式、反三角不等式外，凡含超越式、其他代數式的有限次代數運算及有限次複合的不等式都是(初等)超越不等式。

基本介紹

• 中文名：超越不等式
• 外文名：transcendental inequality
• 所屬學科：數學
• 所屬問題：初等代數（不等式）
• 舉例：指數不等式、對數不等式等

基本介紹

有理不等式和無理不等式統稱代數不等式，除了代數不等式外，還有一類不等式，就是諸如指數不等式、對數不等式、三角不等式、反三角不等式等，統稱為超越不等式，所謂“超越”指的是函式絕不能僅僅依靠對變數實施代數運算而得到，也就是它“超出”代數運算的範圍。

解超越不等式的方法

解上述幾種初等超越不等式，主要有兩種方法：一是將超越函式(指指數函式、對數函式、三角函式、反三角函式等)用新變數代替，此即換元法；另一是利用超越函式(指上述四種函式)的單調性，將其轉化為代數不等式求解，此即函式單調性法。其次還有分類討論法，即當不等式中指數函式或對數函式的底與1比較其範圍不確定時，需對其底進行分類討論，才能求得其解。還有化同底法，當指數與對數不等式中底不相同時，可設法化成同底的指數與對數不等式來解，這裡對數的換底公式是一個很好的工具。其次還可以用圖解法，例如對高次不等式與超越不等式，都可以藉助於函式圖象來求解。例如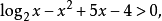原不等式化為令 在同一坐標系中，如圖1，分別作出兩函式的圖象，得兩交點之橫坐標為x₁=1, x₂≈4.5，由此知原不等式的近似解為：1<x<4. 5。

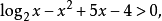
圖1

要正確地變成同解的代數不等式(或不等式組)，就必須熟練掌握這些超越函式的定義和性質。下面分別介紹利用單調性和換元法解超越不等式。

套用函式單調性

【例1】設0<a<1,給出下面四個不等式:

其中不成立的有( )。

A.0個 B.1個C.2個D.4個

解:只(3)不成立(因a/2<a)，故應選B。

【例2】關於x的不等式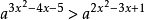的解集為(-2，3)，求實數a的取值範圍。

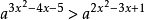
解:顯然(-2，3)是不等式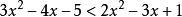的解集，由此知y=a^x是減函式，故a的取值範圍應是(0, 1)。

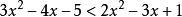
換元法

【例3】解不等式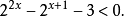

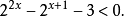
解:原不等式可化為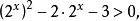

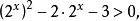
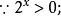
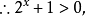
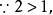
【例4】解不等式

解:原不等式可化為

即

即