誤差修正模型(error correction model,簡記為ECM)是一種具有特定形式的計量經濟學模型,它的主要形式是由Davidson、 Hendry、Srba和Yeo於1978年提出的,稱為DHSY模型。
基本介紹
- 中文名:誤差修正模型
- 外文名:error correction model
- 含義:具有特定形式的計量經濟學模型
- 提出者:Davidson、 Hendry、Srba和Yeo
- 提出時間:1978年
- 學科:統計學
概念
產生原因
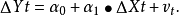
創建模型方法
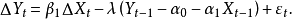
結構
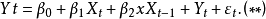

誤差修正模型(error correction model,簡記為ECM)是一種具有特定形式的計量經濟學模型,它的主要形式是由Davidson、 Hendry、Srba和Yeo於1978年提出的,稱為DHSY模型。
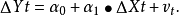
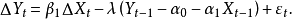
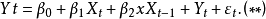
誤差修正模型(error correction model,簡記為ECM)是一種具有特定形式的計量經濟學模型,它的主要形式是由Davidson、 Hendry、Srba和Yeo於1978年提出的,稱為DHSY模型...
閾值誤差修正模型中閾值設定的研究及套用是一篇博士論文,郭建平著。...... 本文以協整與誤差修正理論為基礎,結合結構突變問題的研究方法與閾值類模型的研究內容,考慮外...
二、面板協整檢驗和誤差修正模型第5節 軟體命令第5章 面板受限因變數模型第1節 二元選擇模型第2節 靜態面板離散選擇模型一、二元選擇模型...
數量經濟模型是經濟建模理論、建模方法研究。1.經濟建模理論、建模方法研究。包括古典巨觀經濟模型、協整理論與誤差修正模型、投入產出模型、可計算一般均衡(CGE)模型...
但是電離層的折射、散射效應以及對流層的折射效應都具有一定的變化規律,通過建立合適的傳播誤差修正模型,這些誤差是可以修正到相當好的程度。...
在巨觀經濟計量分析中,Granger(1987)所提出的協整方法已成為了分析非平穩經濟變數之間數量關係的最主要工具之一,且通過線性誤差修正模型(ECM)刻畫了經濟變數之間的...
設計了七個實驗,包括線性回歸模型套用,簡單外推模型套用,平滑技術和季節調整,隨機時間序列的特徵觀察,單位根檢驗、協整與誤差修正模型,ARMA模型套用和條件異方差模型...
3.2.6 誤差修正模型 …… 第4章 微觀計量經濟學模型 第5章 面板數據計量經濟學模型 第6章 非參數計量經濟學模型 第7章 空間計量經濟學模型 參考文...
本章參考文獻第9章 協整與誤差修正模型導讀9.1 協整與誤差修正模型的基本定義9.2 Engle-Granger協整分析方法9.3 向量ADF模型與協整分析9.4 向量誤差修正模型(VECM)...
《上網電價波動對中國火電產業利潤的影響:基於協整檢驗和誤差修正模型的實證分析》,《經濟學動態》,2012.4《上網電價波動對中國火電產業發電量的影響:基於協整檢驗...
該書作為系列教材的一種,著重討論經典的ARMA模型,同時又對最新的時間序列模型加以介紹,例如ARCH模型族(自回歸條件異方差模型)、ECM模型(誤差修正模型)和處理高頻...
序列分析的最新發展成果,諸如樣本區間外預測方法、非線性時間序列模型、Monte ...6.3協整與誤差修正模型 3126.4協整檢驗:Engle—Granger檢驗方法 319...
【實驗總結】實驗十四 Panel Data模型【實驗目的與要求】【實驗準備】【實驗內容】【實驗數據】【實驗步驟】【實驗總結】實驗十五 誤差修正模型【實驗目的與要求】...
模型,著重探討中國出口貿易的環境效應,以期為中國出口貿易管理與相關環境規制提供理論支持;第五章首先採用誤差修正模型分析環境規制對中國出口的影響,其次運用VAR模型對...
14.胥巍,曹正勇,傅新紅.我國東、西部財政支農對農業經濟成長貢獻的比較研究---基於協整分析與誤差修正模型,軟科學(CSSCI),2008.515.李紅梅,傅新紅,吳秀敏.農戶...
很少有基於計量經濟模型與EViews軟體,從論文寫作的角度,將計量經濟模型構建、經濟...第6章 深圳成指與國際股票指數之間的聯動作用研究--基於協整檢驗與誤差修正模型...
中美股票市場信息衝擊的非對稱性調整特徵與聯動性效應—基於門限協整的誤差修正模型究[J],浙江社會科學,2016年第9期第59-65頁。[35] 宋玉臣,臧雲特. 投資者...
第一章是本文的緒論,主要探討文章的選題及文獻回顧;而第二章是對協整和誤差修正模型理論的一個簡要總結;第三章則對平穩面板數據模型進行了概括。文章的第二部分是...
24、周端明、王亞玄:二元性與中國城鄉居民收入差距的演進:協整檢驗與誤差修正模型,《銅陵學院學報》2010年第5期;23、周端明:中國的漸進改革與鄉村工業的轉型,《當代...
該書作為系列教材的一種,著重討論經典的ARMA模型,同時又對最新的時間序列模型加以介紹,例如ARCH模型族(自回歸條件異方差模型)、ECM模型(誤差修正模型)和處理高頻...
74 誤差修正模型 214習題7 216第8章異方差時間序列模型 21981簡單異方差模型 219811異方差的現象 219812方差齊性變換 22182自回歸條件異方差模型 224...
《我國科技型中小企業融資結構微觀影響因素研究——基於協整及誤差修正模型方法》,《東北師大學報(哲學社會科學版)》2012年第04期 《人民幣匯率波動的非對稱機制研...
第9章 向量自回歸和向量誤差修正模型第10章 利用橫截面和時間序列數據的計量模型第11章 狀態空間模型和卡爾曼濾波第12章 聯立方程模型的估計與模擬附錄A EViews...
李凱傑,曲如曉:技術進步對中國碳排放的影響——基於向量誤差修正模型的實證研究,《中國軟科學》2012(6):51-58 李凱傑,曲如曉:碳排放交易體系初始排放權分配機制的...
