簡介 褶積(又名卷積)和
反褶積 (又名去卷積)是一種積分變換的數學方法,在許多方面得到了廣泛套用。用褶積解決試井解釋中的問題,早就取得了很好成果;而反褶積,直到最近,Schroeter、Hollaender和Gringarten等人解決了其計算方法上的穩定性問題,使反褶積方法很快引起了試井界的廣泛注意。有專家認為,反褶積的套用是試井解釋方法發展史上的又一次重大飛躍。他們預言,隨著測試新工具和新技術的增加和套用,以及與其它專業研究成果的更緊密結合,試井在油氣藏描述中的作用和重要性必將不斷增大。
基本內涵 簡單定義:設:
f (
x ),
g (
x )是R1上的兩個可積函式,作
積分 :
可以證明,關於幾乎所有的實數x ,上述積分是存在的。這樣,隨著x 的不同取值,這個積分就定義了一個新函式h(x) ,稱為函式f 與g 的卷積,記為h(x)=(f*g)(x) 。
容易驗證,
(f * g)(x) = (g * f)(x) ,並且
(f * g)(x) 仍為
可積函式 。這就是說,把卷積代替乘法,L1(R1)空間是一個代數,甚至是巴拿赫代數。
卷積與傅立葉變換有著密切的關係。利用一點性質,即兩函式的傅立葉變換的乘積等於它們卷積後的傅立葉變換,能使
傅立葉分析 中許多問題的處理得到簡化。
由卷積得到的函式
f*g 一般要比
f 和
g 都光滑。特別當
g 為具有
緊緻 集的
光滑函式 ,
f 為局部可積時,它們的卷積
f * g 也是光滑函式。利用這一性質,對於任意的
可積函式 f ,都可以簡單地構造出一列逼近於
f 的
光滑函式 列
fs ,這種方法稱為函式的光滑化或
正則化 。
定義 卷積是兩個變數在某範圍內相乘後求和的結果。如果卷積的變數是序列x(n)和h(n),則卷積的結果
,
序列的卷積和 其中星號*表示卷積。當時序n=0時,序列h(-i)是h(i)的時序i取反的結果;時序取反使得h(i)以縱軸為中心翻轉180度,所以這種相乘後求和的計算法稱為卷積和,簡稱卷積。另外,n是使h(-i)位移的量,不同的n對應不同的卷積結果。
如果卷積的變數是函式x(t)和h(t),則卷積的計算變為
,
函式的卷積積分 其中p是積分變數,積分也是求和,t是使函式h(-p)位移的量,星號*表示卷積。
性質 各種卷積運算元都滿足下列性質:
令x(t)*h(t)=y(t),a為任意常數或復常數,則卷積有如下性質:
x(t)*[g(t)+h(t)] = x(t)*g(t)+x(t)*h(t)
x[k]*(g[k]+h[k]) = x[k]*g[k]+x[k]*h[k]
[x(t)*g(t)]*h(t) = x(t)*[g(t)*h(t)]
{x[k]*g[k]}*h[k] = x[k]*{g[k]*h[k]}
a[x(t)*h(t)]=[ax(t)]*h(t)=x(t)*ah(t)
x[k-n]*h[k-l] = y[k-(n+l)]
y'(t)=x'(t)*h(t) = x(t)*h'(t)
常見函式的卷積積分 在信號分析中,以下卷積積分的結果會比較常用:
在卷積運算中,如果能運用以上結論,將大大簡化積分運算,節省解題時間。
卷積定理 卷積定理 指出,函式卷積的
傅立葉變換 是函式傅立葉變換的乘積。即,一個域中的卷積相當於另一個域中的乘積,例如
時域 中的卷積就對應於
頻域 中的乘積。
perfect spaces卷積混響 F[g(x)*f(x)] = F[g(x)]F[f(x)]
利用卷積定理可以簡化卷積的運算量。對於長度為
n 的序列,按照卷積的定義進行計算,需要做2
n - 1組對位
乘法 ,其計算複雜度為;而利用
傅立葉變換 將序列變換到頻域上後,只需要一組對位乘法,利用傅立葉變換的
快速算法 之後,總的計算複雜度為。這一結果可以在快速
乘法 計算中得到套用。
群上卷積 對於這些群上定義的卷積同樣可以給出諸如卷積定理等性質,但是這需要對這些群的表示理論以及調和分析的Peter-Weyl定理。
套用 卷積在工程和數學上都有很多套用:
介紹一個實際的機率學套用例子。假設需求到位時間的到達率為poisson(λ)分布,需求的大小的分布函式為D(.),則單位時間的需求量的分布函式為 F(x):
卷積套用 其中 D(k)(x)為k階卷積。
卷積是一種線性運算,圖像處理中常見的mask運算都是卷積,廣泛套用於圖像濾波。castlman的書對卷積講得很詳細。
高斯變換就是用高斯函式對圖像進行卷積。高斯運算元可以直接從離散
高斯函式 得到:
for(i=0; i<N; i++) 再除以 sum 得到歸一化運算元
N是濾波器的大小,delta自選
首先,在提到卷積之前,必須提到卷積出現的背景。卷積是在
信號與線性系統 的基礎上或背景中出現的,脫離這個背景單獨談卷積是沒有任何意義的,除了那個所謂褶反
公式 上的數學意義和積分(或求和,離散情況下)。
信號與線性系統 ,討論的就是信號經過一個線性系統以後發生的變化(就是輸入 輸出 和所經過的所謂系統,這三者之間的數學關係)。所謂線性系統的含義,就是,這個所謂的系統,帶來的輸出信號與輸入信號的數學關係式之間是線性的運算關係。
因此,實際上,都是要根據我們需要待處理的信號形式,來設計所謂的系統傳遞函式,那么這個系統的傳遞函式和輸入信號,在數學上的形式就是所謂的卷積關係。
卷積關係最重要的一種情況,就是在信號與線性系統或
數位訊號處理 中的卷積定理。利用該定理,可以將
時間域 或空間域中的卷積運算等價為
頻率域 的相乘運算,從而利用FFT等快速算法,實現有效的計算,節省運算代價。
C++語言代碼:
void convolution(double *input1, double *input2, double *output, int mm, int nn) 地震中的套用 地震勘探中,在地表激發點激發的地震子波(seismic wavelet)向地下傳播,當遇到地下波阻抗界面時,一部分能量就會作為反射地震波向上反射回地表,被地面的感測器接收,隨著地震波不斷向下傳播、反射、接收,就會記錄一系列時間延遲的地震波(大地濾波後的地震子波),稱為地震記錄.
這一過程或地震記錄可以用數學模型描述.如果假設地下介質為古皮奧(Goupilaud)的水平層狀介質模型,子波為雷克(Ricker)子波,地震記錄可以看作是由震源子波與地下反射率函式、多次反射、儀器等諸多因素的相褶
積的過程,令x(t),w(t)和n(t)分別表示地震記錄,地震子波及噪聲,褶積過程數學模型描述為:
公式 長期以來,褶積模型廣泛用於描述地震信號.顧名思義,反褶積就是褶積的逆過程,從地震記錄x(t)中恢復出反射率函式r(t).

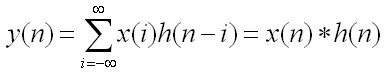 序列的卷積和
序列的卷積和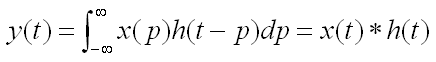 函式的卷積積分
函式的卷積積分







































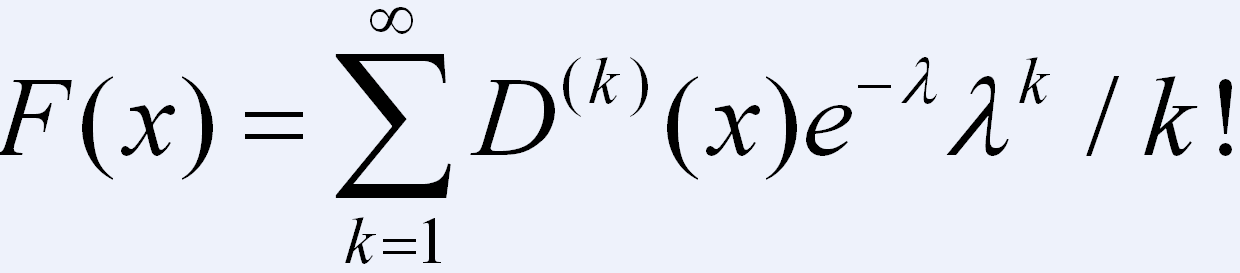 卷積套用
卷積套用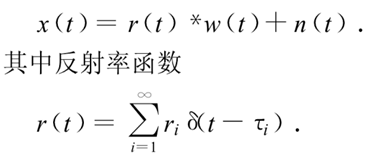 公式
公式




 perfect spaces卷積混響
perfect spaces卷積混響 卷積與相關分析
卷積與相關分析