在泛函分析中,卷積、旋積或摺積(英語:Convolution)是通過兩個函式f 和g 生成第三個函式的一種數學運算元,表征函式f 與g經過翻轉和平移的重疊部分的面積。卷積方程(convolution equation)一種最常見的奇異積分方程。
基本介紹
- 中文名:卷積方程
- 外文名:convolution equation
- 領域:數學
- 性質:奇異積分方程
- 分類:第一類、第二類
- 元素:卷積運算元
卷積
卷積方程
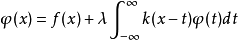

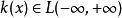
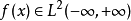
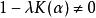
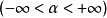

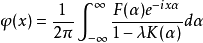

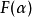
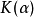
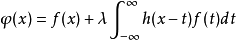
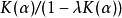
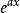
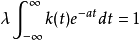
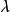
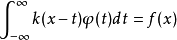


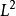


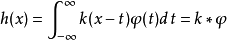
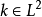
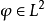
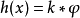
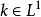
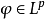
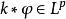
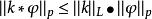
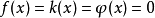

在泛函分析中,卷積、旋積或摺積(英語:Convolution)是通過兩個函式f 和g 生成第三個函式的一種數學運算元,表征函式f 與g經過翻轉和平移的重疊部分的面積。卷積方程(convolution equation)一種最常見的奇異積分方程。
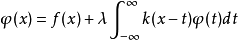

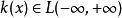
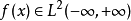
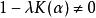
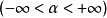

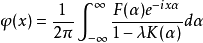

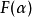
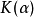
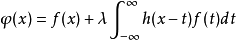
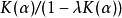
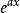
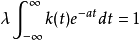
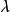
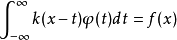


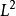


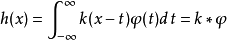
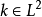
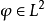
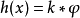
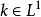
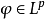
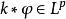
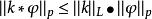
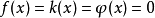

在泛函分析中,卷積、旋積或摺積(英語:Convolution)是通過兩個函式f和g 生成第三個函式的一種數學運算元,表征函式f與g經過翻轉和平移的重疊部分的面積。卷積方程(...
卷積型積分方程(co nvolution type integral e-quation)亦稱差核積分方程,是卷積方程的推廣.它是指以下的奇異積分方程: 此類方程同樣滿足諾特定理.它可通過傅立葉...
卷積定理是傅立葉變換滿足的一個重要性質。卷積定理指出,函式卷積的傅立葉變換是函式傅立葉變換的乘積。具體分為時域卷積定理和頻域卷積定理,時域卷積定理即時域內...
卷積是分析數學中一種重要的運算。設f(x), g(x)是R1上的兩個可積函式,作積分:可以證明,關於幾乎所有的x∈(-∞,∞) ,上述積分是存在的。這樣,隨著x的不...
在數學中,反卷積是一種基於算法的過程,用於反轉卷積對記錄數據的影響。 反卷積的概念廣泛用於信號處理和圖像處理技術。 由於這些技術反過來在許多科學和工程學科中...
《反卷積和信號復原》是2001年3月1日國防工業出版社出版的圖書。... 其中包括:導論;數學基礎;Fredholm第一類積分方程的解、規整化和計算模型;一維信號反卷積和...
泊松方程是數學中一個常見於靜電學、機械工程和理論物理的偏微分方程。是因法國數學家、幾何學家及物理學家泊松而得名的。泊松首先在無引力源的情況下得到泊松方程...
維納-霍普夫方程是一類特殊的積分方程,它是使連續時間平穩過程的方差估計誤差達到極小的最優濾波器脈衝回響函式滿足的必要條件。...
《積分方程(第3版)》是2012年由沈以淡編著,清華大學出版社出版的一本書籍。... 5.1 用Fourier變換解卷積型Fredholm積分方程1125.2 用Laplace變換解積分方程117...
《廣義函式與數學物理方程》是1999年高等教育出版社出版的圖書,作者是齊民友。本書主要介紹了廣義函式與數學物理方程的基本內容和規律技巧。...
為了求解卷積方程,施瓦茲通過傅立葉變換將其轉化為乘積方程。這就需要定義分布的傅立葉變換,進而他引入了施瓦茲空間,從而解決了卷積方程的求解問題。他的這一研究...
8.5.2 沃爾泰拉卷積型積分方程8.6 多項式類型的積分方程8.6.1 只含多項式的弗雷德霍姆積分方程的解法8.6.2 母函式法習題參考文獻第9章 數論在物理逆問題中的套用...
方程(7)可以通過時域分析法或頻域分析法求解。時域分析法是利用卷積積分給出方程(7)的解,可用於任意變化的載荷情況。頻域分析法是利用傅立葉分析把周期性載荷展開...
