聯絡形式(connection forms)特徵聯絡的1次形式。
基本介紹
- 中文名:聯絡形式
- 外文名:connection form
- 所屬學科:纖維叢理論
定義

性質
簡介

聯絡形式(connection forms)特徵聯絡的1次形式。


共同犯罪的意思聯絡是共犯人之間意志的傳遞和交流,意思聯絡並不局限於犯罪預謀,後者在謀劃意圖上更加完整和深入,也更加具體全面,但在時間界限上是趨前的,可認為是雙向對合的意思聯絡形式之一。意思聯絡通常並不是策劃具體的犯罪計畫,而...
撓率形式是刻畫聯絡對稱性的二次形式。設(M,)是n維仿射聯絡空間,{ωⁱ}是定義在開鄰域U M上的局部余標架場,ω是相應的聯絡形式。若Ωⁱ=dωⁱ-ω∧ωⁱ,則Ωⁱ是定義在U上的二次外微分式,稱為撓率形式。直接計算...
微分幾何中,埃雷斯曼聯絡(Ehresmann connection)是套用於任意纖維叢的聯絡概念的一個版本。特別的是,它可以是非線性的,因為一般的纖維叢上沒有合適的線性的概念。 一般情況下,它適用於主叢這一類特殊的纖維叢,通過聯絡形式表述,...
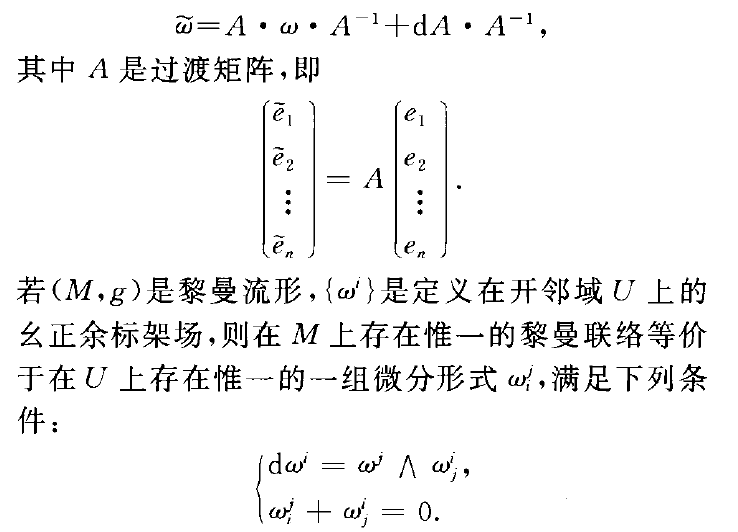
式中gjk,gil是黎曼流形上度量張量的反變和協變形式。上述的平行移動、曲率等概念就和黎曼幾何中的意義相一致。如不採取自然標架,而採取另外的基{ei},利用(5)就可以得到相應的聯絡形式。特別,如選取ei,使它們在各點都是單位、正交...
在黎曼流形和偽黎曼流形的理論中,共變導數一詞經常用於列維-奇維塔聯絡。聯絡的坐標空間的表達式稱為克里斯托費爾符號。黎曼幾何 微分幾何中,黎曼幾何(英語:Riemannian geometry)研究具有黎曼度量的光滑流形,即流形切空間上二次形式的...
設ξ:E→M為向量叢,則M的取值於ξ的微分k形式為叢Hom(Λₖ(T*M),ξ)的截面,這些截面的集記為Aₖ(M,ξ)。相關概念 設η:P×𝖌→P為平凡叢,聯絡形式ω∈A₁(P,η),曲率形式Ω∈A₂(P,η)。微分r形式全體...
設P是一個以流形M為底空間、李群G為結構群的主纖維叢.屍上的一個聯絡A可局部地用一個取值於G的李代數中的1形式A=A淚x0戈表出,其中x0是流形M的局部坐標,X是G的李代數的一組基.重疊區域U,門Uz上的兩個局部聯絡1形式A,...
然後計算這些運算元的Rankin-Cohen Bracket,並希望以此來證明Bump關於Siegel模形式導數的一個猜想。為了給出這些自守型的全純導數運算元,我們需要在對應的空間上構造比聯絡更弱的所謂的模聯絡。我們還將用聯絡來研究Theta級數的導數以及它滿足...
聯絡員是一種工作崗位,該崗位主要負責聯絡和服務工作,做好領導安排的工作和匯報工作。簡要介紹 聯絡員的工作可用四個字概括,即“聯絡、服務”,但歸根到底是“服務”二字,因為,聯絡也是服務的一種形式。領導有的也配備專門的聯絡員...
聯絡單元組織 聯絡單元組織(associated unit organization),與相關課程相應的教材組織形式。聯絡兩種或幾種相互之間有關係的學科,採用單元教學法或設計教學法組織教學活動。
(三)承擔聯絡員會議議定事項的組織協調工作。(四)根據聯絡員會議各成員單位要求,協調生產安全事故災難應急救援有關工作。第五條實行聯絡員例會制度。(一)聯絡員例會為聯絡員會議基本形式,原則上每半年召開一次,會議的主要任務是:...
調和形式(harmonic form)一類最重要的向量叢值的外微分形式.設。是向量叢值的p形式,。表示霍奇一拉普拉斯運算元.若乙。一。,則稱。為向量叢值的調和p形式.換言之,當。E ker△時,稱。為調和形式.當底流形M為緊緻無邊時,。為...
connection,英語單詞,名詞,意思是“連線;關係;人脈;連線件”。單詞發音 英 [kəˈnekʃn] 美 [kəˈnekʃn]短語搭配 connection form [數] 聯絡形式 ; 連線形式 Cartan connection 嘉當聯絡 ; 加當聯絡 ; 卡當聯絡...
撓率形式,是撓率的另一種刻畫,適用於M的標架叢FM。這個主叢裝備有一個聯絡形式ω,一個gl(n)-值的 1-形式將豎直矢量映到gl(n) 中的右作用的生成元,且通過在gl(n) 上的伴隨表示等變糾纏於 GL(n) 在 FM的切叢上的右作用...
焊接形式是用一個從M的切叢到配向量叢的典範同構將G-結構下面的G叢繫於流形自身的局部幾何上。儘管焊接形式不是一個聯絡形式,經常可以視為一個聯絡形式的前身。 詳細說來,假設Q是G-結構的主叢。如果Q是實現為M的切叢的壓縮,那么...
取P中任何聯絡形式w,設 為相伴的曲率2-形式。若 是k次齊次多項式,設{\displaystyle f(\Omega )}是P上的2k-形式,以下式給出 其中 是2k個數的對稱群 中置換 的符號。(見Pfaffian)。可證 是閉形式,故 且 的德拉姆上同調...
