主纖維叢上的聯絡(connection on the principalbundle)主纖維叢中鄰近兩點間的一種對應關係，藉此可定義纖維中的一點沿底空間中的一條曲線的平行移動.
設P是一個以流形M為底空間、李群G為結構群的主纖維叢.屍上的一個聯絡A可局部地用一個取值於G的李代數中的1形式A=A淚x0戈表出，其中x0是流形M的局部坐標，X是G的李代數的一組基.重疊區域U,門Uz上的兩個局部聯絡1形式A，和AZ之間存在著關係式
主纖維叢上聯絡
相關詞條
- 主纖維叢上聯絡
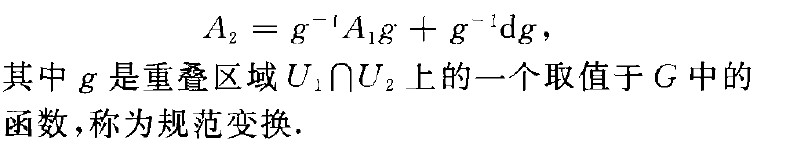
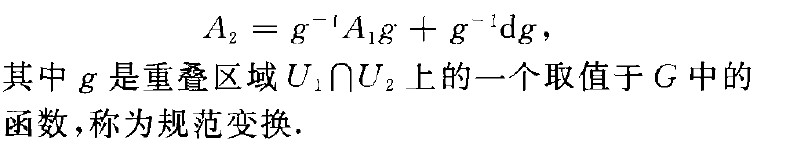
主纖維叢上的聯絡(connection on the principalbundle)主纖維叢中鄰近兩點間的一種對應關係，藉此可定義纖維中的一點沿底空間中的一條曲線的平行移動.設P是一個以流形M為底空間、李群G為結構群的主纖維叢.屍上的一個聯絡A可局部地...
- 聯絡論
實際上，規範勢相當於聯絡，場的強度相當於曲率，截面相當于波函式，示性數表示某些物理量（如磁荷，瞬子數等）。20世紀70年代起，纖維叢聯絡論和規範場論的相互溝通對數學和物理學都起了巨大的推進作用。
- 主纖維叢
主纖維叢簡稱為主叢，簡記為P（M,G）或P。定義 主纖維叢（principal fiber bundle）由一個叫叢流形（bundle manifold）的流形P，一個叫做底流形（base manifold）的流形M和一個叫做結構群（structure group）的李群G組成，滿足以下要求...
- 埃雷斯曼聯絡
微分幾何中，埃雷斯曼聯絡（Ehresmann connection）是套用於任意纖維叢的聯絡概念的一個版本。特別的是，它可以是非線性的，因為一般的纖維叢上沒有合適的線性的概念。 一般情況下，它適用於主叢這一類特殊的纖維叢，通過聯絡形式表述，...
- 纖維叢
1937年美國數學家惠特尼把流形及以其上每一點為原點的線性獨立的切向量組全體總括在一起而得到纖維叢的概念。他還證明了微分流形的嵌入定理，正式創立微分拓撲學。1946年陳省身認識到E.嘉當的聯絡的幾何學思想與纖維叢理論有密切關係，...
- 楊一米爾斯規範理論
楊一米爾斯規範理論是一種關於主纖維叢上聯絡的理論 楊一米爾斯規範理論(Yang-Mills gauge the-ory)一種關於主纖維叢上聯絡的理論.楊振寧和米爾斯(Mills , R. L.)於1954年提出的一種規範理論.它起源於電磁場理論，並已成功地用來...
- 陳一西蒙斯規範理論
陳-西蒙斯理論（Chern-Simons theory）由陳省身和詹姆斯·西蒙斯所提出的一種規範理論。它是關於在三維底流形的主纖維叢上聯絡的理論。這種理論對三維流形和扭結的拓撲性質的研究起了十分重要的作用。陳一西蒙斯理論（Chern-Simons theory）...
- 和樂群
當γ取遍所有以x為基點的閉環路後，這些相應的元素g的全體就構成了G的一個子群H，稱為主纖維叢上該聯絡的和樂群。若γ限於以x為基點的同倫於零的閉環路，則相應的元素g的全體就構成了G的另一個子群H，稱為該聯絡的齊次和樂群...
- 黎曼幾何引論
本書較好地反映了這種緊密的聯繫，其內容共有三章，包括Kahler流形、黎曼對稱空間及主纖維叢上的聯絡。每章末都附有大量的習題，書末並附有習題解答和提示，便於讀者深入學習和自學。本書的選材和敘述都有它獨到之處，與現有的數學...
- 黎曼幾何引論(下)
《黎曼幾何引論（下）》較好地反映了這種緊密的聯繫，其內容共有三章，包括Kahler流形、黎曼對稱空間及主纖維叢上的聯絡。每章末都附有大量的習題，書末並附有習題解答和提示，便於讀者深入學習和自學。《黎曼幾何引論（下）》的選材和...
- 陸啟鏗
70年代指出物理上規範場與數學上的主纖維叢的聯絡的關係，證明楊振寧的規範場的積分定義等價於沿一曲線的平行移動80年代以來，提出一個系統的方法，可具體地構造非緊對稱空間的熱核。學術論著 1956年，發表於《數學進展》的近百頁綜合性...
- 微分幾何基礎(第一卷)
1.5 纖維叢 二章 聯絡理論 2.1 主纖維叢上的聯絡 2.2 聯絡的存在與擴張 2.3 平行性 2.4 和樂 2.5 曲率形式和結構方程 2.6 聯絡的映* 2.7 約化定理 2.8 和樂定理 2.9 平坦聯絡 2.10 局部和樂與無窮小...
- 電磁勢
p 和勢能V作一定代換即可。在量子力學中，帶電粒子在沒有電磁場的空間中運動時，也會受到電磁勢的作用而改變相位。從現代規範場理論的角度看，電磁場是以U(1)群為規範群的規範場，而電磁勢就是主纖維叢上的聯絡。
- 楊一米爾斯作用量
楊一米爾斯作用量(Yang-Mills action)是一類特殊的泛函。對底空間為四維流形M'，結構群為緊緻單純李群G的主纖維叢屍上的任一聯絡A，有下列泛函 其中F',是聯絡A的曲率，丨FA丨是曲率的模長平方，1是M‘的體積元.YM(A)稱為楊一...
- 微分幾何基礎-第一卷
譯者的話前言各章節之間的依賴關係第一章 微分流形 1.1 微分流形 1.2 張量代數 1.3 張量場 1.4 Lie群 1.5 纖維叢第二章 聯絡理論 2.1 主纖維叢上的聯絡 2.2 聯絡的存在與擴張 2.3 平行性 2.4 和樂群 2.5 曲率形式...
- 數學物理中的微分幾何與拓撲學
de Rham 上同調論 ├第8章 纖維叢及其拓撲結構 ├第9章 纖維叢上的聯絡與曲率 ├第10章 纖維叢的示性類與曲率張量 第3部分 指標定理和四維流形 ├第11章 無邊界流形的指標定理 ├第12章 四維流形的一些重要性質 著作權頁 ...
- 數學物理中的微分形式
《數學物理中的微分形式》是1989年北京航空航天大學出版社出版的一本圖書，作者是韋斯坦霍爾斯(Westenholz,C.V.)。內容介紹 本書包括有:點集拓樸,Rn上的微積分,流形上的微分學,李群,纖維叢,上同調論,聯絡理論等。
- 實用邏輯教程(第3版)
本書以主叢與矢叢上的聯絡為主線介紹現代微分幾何，全書分兩部分，各5章。前3章給出微分流形的基本概念，把歐氏空間的微積分推廣到微分流形上．第4，5章分別討論riemann流形與李群及李代數．第6，7章分別介紹纖維叢理論與複流形，...
