基本介紹
- 中文名:置信度傳播
- 外文名:belief propagation
簡介
歷史
置信度傳播基礎
貝葉斯網路












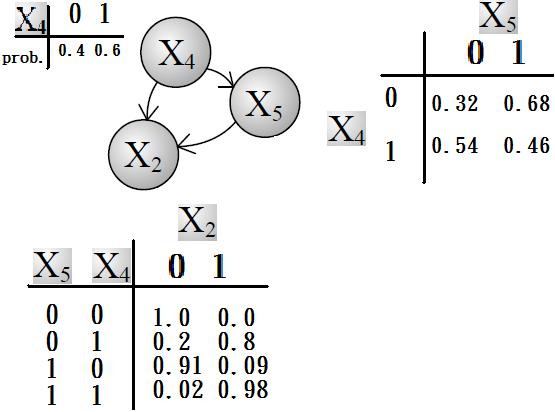













置信度傳播(英語:belief propagation),又稱為乘積和信息傳遞(sum-product message passing),是在貝葉斯網路、馬爾可夫隨機場等機率圖模型中用於推斷的一種信息傳遞算法。簡介在給定...
置信傳播,又名和-積信息傳遞,是一種在圖模型上進行推斷的訊息傳遞算法,可用在貝葉斯網路和馬爾科夫隨機域中。置信傳播由Pearl在1982年最早提出,後來由早期在樹上的建模推廣至在polytree上的套用。置信傳播算法利用結點與結點之間相互傳遞信息而更新當前整個MRF(馬爾科夫隨機場)的標記狀態,是基於MRF的一種近似計算...
,Xn)} = 1-α成立,則稱〔T1,T2〕為θ的區間估計,T1稱為置信下限,T2稱為置信上限,1-α稱為置信度, 〔T1,T2〕稱為置信區間。α越小,1-α就越大, 區間[T1,T2]的距離就越大,θ落在[T1,T2]之間的機率也就越大;反之越小。α的值直接影響著區間估計的置信區間和置信度,α的值太小,估計...
課題組進一步發現符號相關性的丟失導致會比特置信度在多進制Tanner圖傳播時出現劣化,而代數結構能夠指示多進制符號的置信度,因此通過引進漢明距離和符號重數提升了基於比特置信度的多進制LDPC 碼解碼算法性能。課題組通過研究符號置信度與子域置信度的關係,通過保留重要符合相關性,提出了基於子域置信度的多進制LDPC 碼...
用維斯捷利烏斯(Visteliws)置信帶法檢驗一組數據的正態性時,以標準化值ui為中心,以ui±uασui所構成的區間,其中uα為置信係數,σui,為標準化值ui的方差。若全部樣本值落在置信帶內,則以置信度p=1-α認為樣本值來自正態總體。設X1,X2,… ,Xn為來自於分布F(x)的獨立同分布樣本.所謂F(x)的置信帶...
5.4.2 基於等機率方法構建並集置信規則庫 84 5.4.3 基於自組織映射方法構建並集置信規則庫 86 5.4.4 結果對比與討論 87 5.5 結論 89 參考文獻 89 第6章 基於自組織映射的並集置信規則庫傳播方法 90 6.1 基本概念 90 6.2 子置信規則庫權重計算 92 6.3 基於自組織映射的置信度計算 93 6.4 置信...
2.2.3 置信度傳播的基本原理及其套用 23 2.2.4 實用的解碼方法 27 2.2.5 性能的理論分析 29 2.3 準循環LDPC碼(QC-LDPC) 32 2.3.1 擴展矩陣 33 2.3.2 基礎矩陣的基本結構 38 2.3.3 編碼算法 39 2.3.4 準循環LDPC碼的多碼長設計 42 2.3.5 基於QC-LDPC碼的多碼率設計 ...
9.5.1 系統模型195 9.5.2 狀態演化方程196 9.5.3 多水平低位數ADC替換高位數ADC200 9.5.4 仿真結果與分析203 附錄A Appendix A 鬆弛置信度傳播算法推導207 附錄B Appendix B AMP算法推導213 附錄C Appendix C 縮略語217 附錄D Appendix D 縮略語221 參考文獻22 ...
針對沒有布放錨節點的海域中多水下自主航行器的協同定位問題,基於置信度傳播算法,設計了分散式間歇性合作定位方法。針對只有一個錨節點移動出場景,提出了使用期望最大算法進行定位求解的方案。 提出了基於廣播模式的水下目標定位及時間同步方法,可實現水下目標被動定位及時間同步。 搭建了水聲通訊定位硬體在環(...
全流程自動化的生產模式,以數字攝影測量、傾斜攝影測量、計算幾何、計算機圖形學等技術為核心,並結合軟體工程等理論,全面攻克了傾斜影像數據處理難點,研發仿射不變特徵提取、基於內容的影像檢索、ADMM網路分散式平差等先進算法,實現影像鄰接關係快速確立與國際領先的傾斜影像精密空三解算;利用基於置信度傳播的實時密...
提高算法的實時性;針對經典區域增長和動態規劃的共同缺點,在接近垂直的方向上同時進行區域增長和動態規劃,實現多方向平滑約束,進一步提高精度;針對重構的質量判斷,通過可靠度分類和圖像分割結果約束置信度傳播的方向和範圍,最佳化傳播路徑,在提高了結果精度的同時,也降低了計算的複雜度。
3.LPDC碼的滑窗置信度傳播解碼算法(SWBP)4.用於壓縮感知的2D正交匹配追蹤(2D-OMP)5.狀態輔助的誤差彈性熵編碼 榮譽獎勵 1.最佳學生論文獎,AMIA TBI, PALME: PAtients Like My gEnome, 2016 2.科學技術進步三等獎,2016 3.科技技術進步二等獎,2015 4.《中國科學》雜誌年度風雲人物,2015 5.教育部新世紀...
8.2.3 高斯置信度傳播與更新 231 8.2.4 統計線性化 236 8.2.5 算法流程 238 8.2.6 算法仿真 239 8.3 序貫、分散式、貝葉斯協作方法 244 8.3.1 集中式序貫定位 244 8.3.2 基於分散式MMSE濾波的序貫時空協作定位 248 8.3.3 算法仿真與比較 258 8.4 引理 1的證明 261 8.5 引理 2的證明 265...
本書首先對Markov隨機場進行了基本的介紹和描述,圍繞Markov隨機場最關鍵的最大後驗機率MAP推理問題詳細介紹了幾種基本求解方法,主要包括二元離散標記下的圖切割方法、多類標籤下的決策移動法、均值場理論近似求解、環狀置信度傳播法以及線性規劃求解法。同時,在基本方法的基礎上擴展至當前最有挑戰性的研究課題,集中...
告警關聯研究和套用在此基礎上已取得了一些研究成果,如凌緒雄通過頻繁模式(Apriori算法、FP-Growth算法、NHTFPG算法)和序列模式(WINEPI算法)挖掘系統,比較了算法性能並分析了愛立信MSC,MGW ,BSC網元告警之間的相關性;安歡結合置信度分析了關聯模型(Apriori算法)和序列模型挖掘告警信息的價值,但在根據告警重要程度賦予...
1-α 為置信度或置信水平,其表明了區間估計的可靠性。顯著性水平是假設檢驗中的一個概念,是指當原假設為正確時人們卻把它拒絕了的機率或風險。它是公認的小機率事件的機率值,必須在每一次統計檢驗之前確定,通常取α=0.05或α=0.01。這表明,當作出接受原假設的決定時,其正確的可能性(機率)為95%或99%...
1.2.2置信度與置信區間 1.3建模與仿真過程的不確定性與誤差 1.3.1偶然不確定性、認知不確定性及誤差 1.3.2不確定性與誤差的識別與傳播 1.4核反應堆中子輸運問題的套用實例 1.4.1物理系統的概念建模 1.4.2概念模型的數學建模 1.4.3數學模型的離散化及算法選擇 1.4.4編程仿真及數值結果...
美國政府出於軍事目的,把GPS系統設定為兩種級別的服務,其中C/A碼為全球用戶免費使用,但對C/A碼採取人為降低精度的措施——選擇可用性(SA)政策,這樣使得單機定位只能達到100m(平面,95%置信度),這種精度為GPS系統精度,而與GPS接收機無關。因此無論何種GPS接收機,只採用C/A碼定位,精度就只能達到100m。...
來自芬蘭和歐洲量子計算公司IQM的科學家研製出了一種新的超導量子比特“獨角獸”,並以99.9%的置信度利用“獨角獸”實現了量子邏輯門。基本的量子門 量子門常使用矩陣表示,操作K個量子比特的門可以用2 x 2 的酉矩陣表示。 一個門輸入跟輸出的量子比特數量必須要相等。 量子門的操作可以用代表量子門的矩陣與代表...
用數軸上的一段距離或一個數據區間,表示總體參數的可能範圍.這一段距離或數據區間稱為區間估計的置信區間。出發點 區間估計(interval estimation)是從點估計值和抽樣標準誤差出發,按給定的機率值建立包含待估計參數的區間.其中這個給定的機率值稱為置信度或置信水平(confidence level),這個建立起來的包含待估計參數...
一般來講,信號和像素級的融合目的在於增加圖像中的有用信息成分,如提高圖像品質、合理地銳化等;特徵級融合是為了能以較高的置信度提取有用的圖像特徵;決策級融合則允許對來自多個感測器或數據源的信息在最高抽象層上進行處理,以得出最終或輔助的決策。分類 基於像元的圖像融合 基於像元的圖像融合是指對測量的物理...
(5)具有高可靠性。太空飛行器的可靠性由各分系統可靠性組成。對太空飛行器的可靠性一般都要求很高。而空間發動機起動關機次數頻繁,要求推進系統工作可靠性就更高。太空飛行器推進系統可靠性指標要求:一般太空飛行器可靠度為0.98~1.0(置信度0.95).載人太空飛行器為1.0。(6)低成本。推進系統在太空飛行器成本中占有相當大的比例,...
