有向無環圖

有向無環圖指的是一個無迴路的有向圖。如果有一個非有向無環圖，且A點出發向B經C可回到A，形成一個環。將從C到A的邊方向改為從A到C，則變成有向無環圖。有向無環圖的生成樹個數等於入度非零的節點的入度積。

基本介紹

• 中文名：有向無環圖
• 外文名：DAG （Directed acyclic graph）
• 學科：數據結構
• 介紹：無迴路有向圖

描述

在圖論中，如果一個有向圖無法從某個頂點出發經過若干條邊回到該點，則這個圖是一個有向無環圖（DAG圖）。

因為有向圖中一個點經過兩種路線到達另一個點未必形成環，因此有向無環圖未必能轉化成樹，但任何有向樹均為有向無環圖。

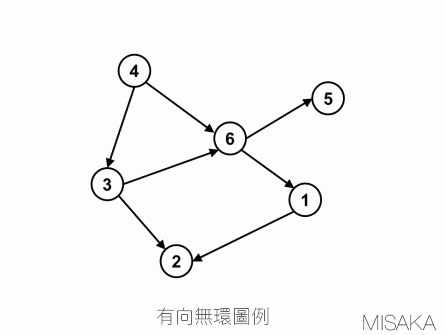有向無環圖

套用

一個無環的有向圖稱做有向無環圖（Directed Acyclic Graph）。簡稱DAG 圖。DAG 圖是一類較有向樹更一般的特殊有向圖，如圖 給出了有向樹、DAG 圖和有向圖的例子。

有向樹、DAG 圖和有向圖的示例

有向無環圖是描述含有公共子式的表達式的有效工具。例如下述表達式：

((a+b)*b*(c+d)+(c+d)*e)*(c+d)*e

可以用第六章討論的二叉樹來表示，如圖1 所示。仔細觀察該表達式，可發現有一些相同的子表達式，如(c+d)和(c+d)*e 等，在二叉樹中，它們也重複出現。若利用有向無環圖，則可實現對相同子式的共享，從而節省存儲空間。例如圖2 所示為表示同一表達式的有向無環圖。

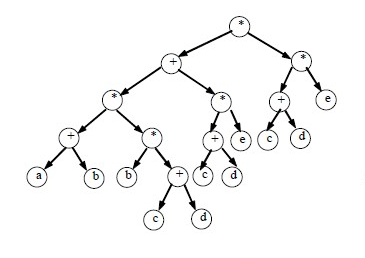用二叉樹描述表達式

檢查一個有向圖是否存在環要比無向圖複雜。對於無向圖來說，若深度優先遍歷過程中遇到回邊（即指向已訪問過的頂點的邊），則必定存在環；而對於有向圖來說，這條回邊有可能是指向深度優先生成森林中另一棵生成樹上頂點的弧。但是，如果從有向圖上某個頂點v 出發的遍歷，在dfs(v)結束之前出現一條從頂點u 到頂點v 的回邊，由於u 在生成樹上是v 的子孫，則有向圖必定存在包含頂點v 和u 的環。

有向無環圖是描述一項工程或系統的進行過程的有效工具。除最簡單的情況之外，幾乎所有的工程（project）都可分為若干個稱作活動（activity）的子工程，而這些子工程之間，通常受著一定條件的約束，如其中某些子工程的開始必須在另一些子工程完成之後。
對整個工程和系統，人們關心的是兩個方面的問題：一是工程能否順利進行：二是估算整個工程完成所必須的最短時間。這樣兩個問題都是可以通過對有向圖進行拓撲排序和關鍵路徑操作來解決的。

描述表達式的有向無環圖