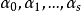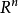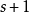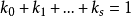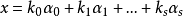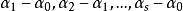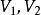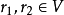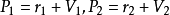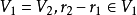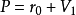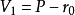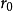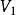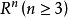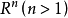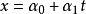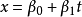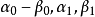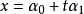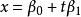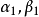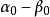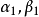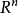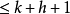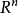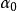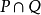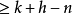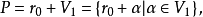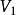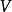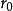線性流形

線性流形(linear manifold)是幾何學中的常用概念，即Pⁿ中的直線，二維平面，三維平面，…，n-1維平面的統稱。設A是線性空間R中的真子集，若對x,x'∈A，θ,θ'∈K，θ+θ'=1，必有θx+θ'x'∈A，就稱A是線性流形。設M是R中的線性子空間，x₀是R中一點，則集M+x₀是一線性流形；反之，每一線性流形可表成M+x₀的形式。 線性流形表示式A=M+x₀中的子空間M，稱做A的平行子空間。若兩個線性流形A和B具有相同的平行子空間，就說A和B相互平行。以經0點的直線L₀作為平行子空間的線性流形L叫做直線， 以經0點的超平面P₀作為平行子空間的線性流形P叫做超平面。兩個相互平行的線性流形必或是重合，或是不相交。線性空間中的線性流形是平行子空間的一個平移，而超平面是全空間中的最大線性流形。當人們想把整個空間劃分成各個區域時，套用超平面的概念，將使其幾何形象特別鮮明。

基本介紹

• 中文名：線性流形
• 外文名：linear manifold
• 所屬學科：數學
• 相關概念：線性空間，超平面等

基本介紹

所謂線性空間V的線性流形，即為

其中 是 的子空間， 是V的固定向量，且 的維數稱為線性流形P的維數，一維線性流形稱為直線，二維線性流形稱為平面，更高維的線性流形稱為超平面。

相關性質

定理1 設 是 的任意 個向量，且 ，則形如

的所有向量組成一個維數等於向量組 的秩的線性流形P。

定理2 是V的子空間，而 ，則 相等的充要條件是。

由線性流形定義的關係式 或 可看出，線性流形P是從線性子空間平行移動一個向量 所得，而定理2則說明，用平行移動得到所給流形P的那個線性空間 是唯一確定的。

定理3 中任意兩條直線包含在某個三維線性流形中。

定理4 空間 的兩條直線 和 位於一個平面內的充要條件是 線性相關。

推論1 兩條直線 和 穿過一點但不重合的充要條件是 線性無關，而 可用 線性表出。

定理5 空間 的兩個維數分別為k和h的線性流形P和Q包含在一個維數 的線性流形中。

定理6 如果空間 的兩個維數分別為k和h的線性流形P和Q有一個公共向量 ，則 是一個維數 的線性流形。