等角共圓定理

等角共圓定理 若線段同側二點到線段兩端點連線夾角相等，那么這二點和線段二端點四點共圓。

等角共圓定理是四點共圓的基本判定方法之一，可以看做是定理“等弧所對圓周角相等”的逆定理。

基本介紹

• 中文名：等角共圓定理
• 套用學科：數學
• 適用領域範圍：數學-（曲線）幾何

定律定義

若線段同側二點到線段兩端點連線夾角相等，那么這二點和線段二端點四點共圓。這是等角共圓定理的基本簡單描述。此定理也可以描述為：把被證共圓的四個點連成共底邊的兩個三角形，且兩三角形都在這底邊的同側，若能證明其頂角相等，即可肯定這四點共圓。

推導過程

證法一

（反證法）

由不在同一直線的三點能確定一個圓，可以以點A、B、C確定一個圓（即為⊙O），接下來只要證明點D也在⊙O上即可。

先證引理若點D不在⊙O上，∠D≠∠C：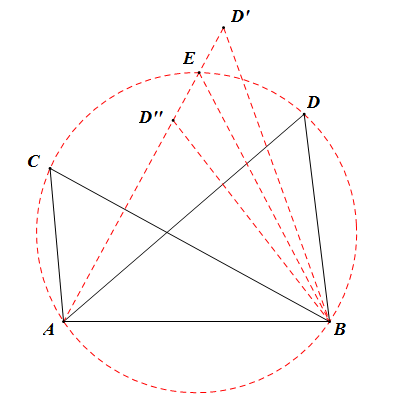

以A為端點引出一條射線交⊙O於點E，在射線AE上任取兩點D'和D''，使D'在圓外，D''在圓內，連結BE。

由三角形外角定理，得：

∠AD'B=∠AEB-∠D'BE<∠AEB=∠D；

∠AD''B=∠AEB+∠D''BE>∠AEB=∠D，

即∠AD'B<∠D,∠AD''B>∠D，

亦即若點D不在⊙O上，∠D≠∠C，引理得證。

再證原命題：假設點D不在⊙O上，則∠D≠∠C，與條件∠D=∠C不符，

故假設不成立，則A、B、C、D四點共圓，原命題得證。

證法二

（三角函式法/解直角三角形）

如圖，作△ABC的外接圓⊙O，過點O作OH⊥AB於點H,連結OA、OB，

當點C、D與線段AB在其外接圓的同側時，

易得∠1= ∠AOB=180°-∠C，

∴⊙O的半徑 AH÷sin (180°-∠C)=AB÷2sin (180°-∠C)；

同理可得△ABD的外接圓半徑 AB÷2sin (180°-∠D)。

故△ABC和△ABD的外接圓半徑相等，且都經過A、B兩點，

又∵點C、D在AB的同側，∴△ABC和△ABD的外接圓重合，

即A、B、C、D四點共圓。

當點C、D與線段AB在其外接圓的異側時，

可以類似地得到A=AB÷2sin C，

又，

故可知確定共底AB的長和相等角的度數即可確定這四點所在的圓。