同圓或等圓中的三角形面積比等於三邊乘積之比
基本介紹
- 中文名:共圓定理
- 外文名:Circular theorem
- 表達式:S1:S2=a1*b1*c1:a2*b2*c2
- 套用學科:數學
- 適用領域範圍:數學
證明
情況1
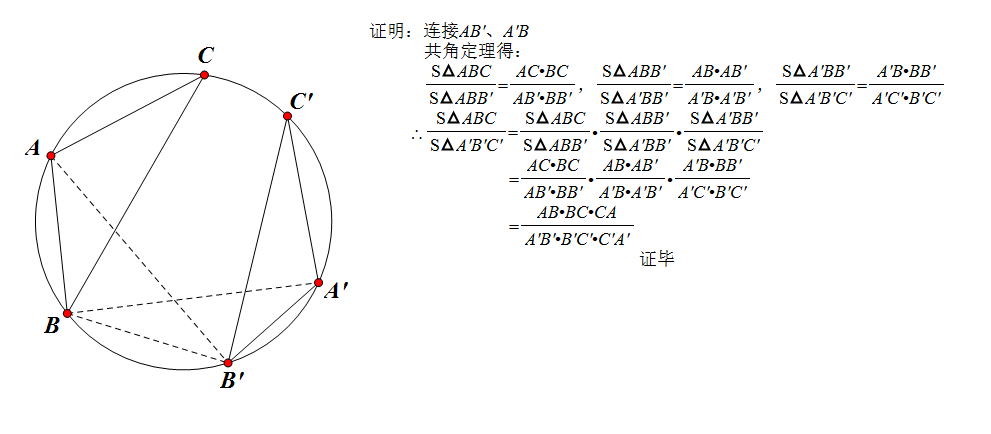
情況2
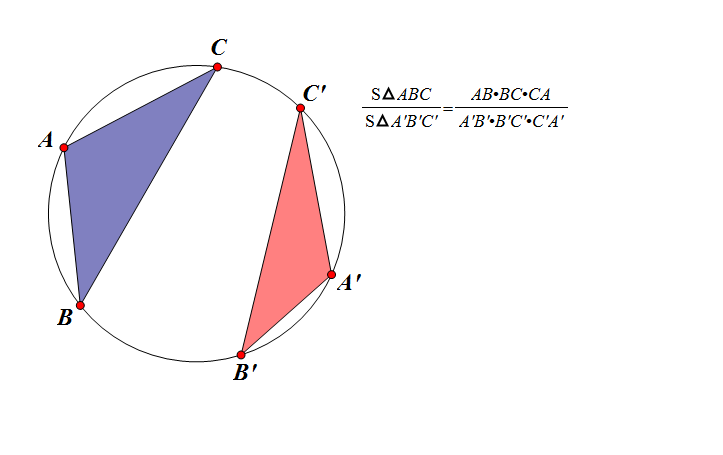
套用
 蝴蝶定理
蝴蝶定理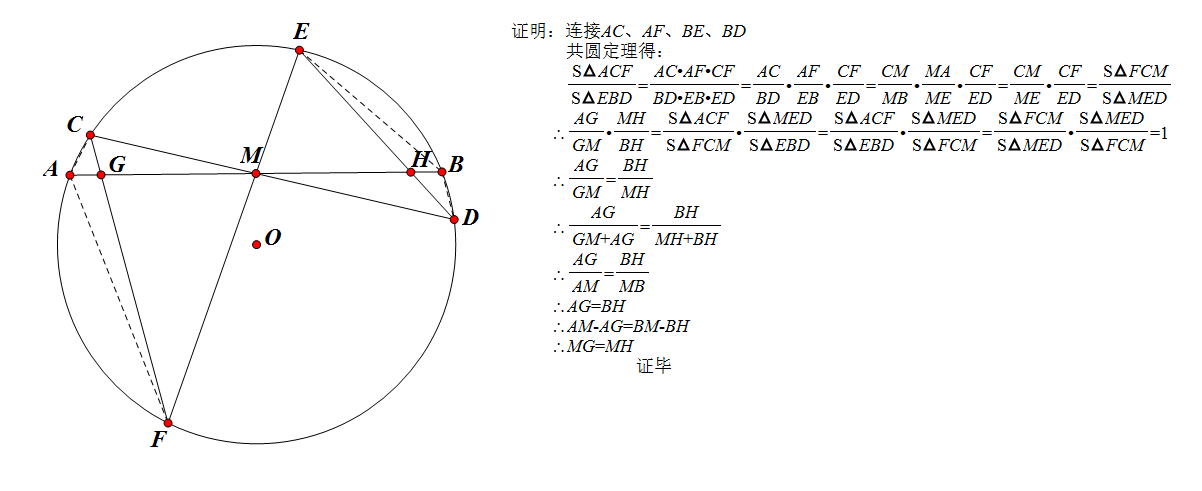 用面積法證明蝴蝶定理
用面積法證明蝴蝶定理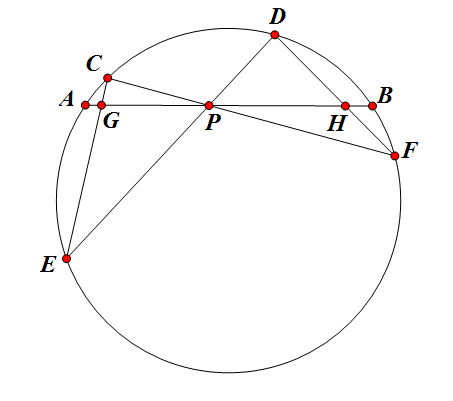 坎迪定理
坎迪定理 用面積法證明坎迪定理
用面積法證明坎迪定理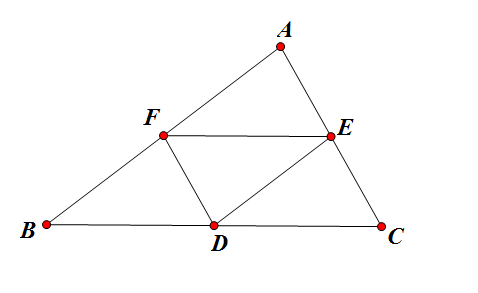 例題
例題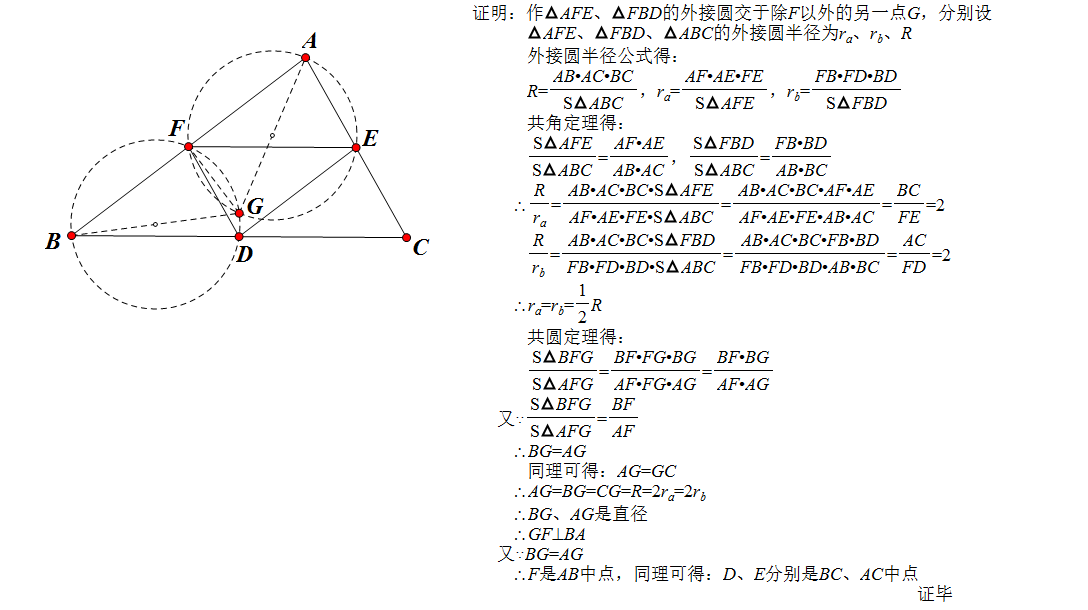 例題證明
例題證明
同圓或等圓中的三角形面積比等於三邊乘積之比


 蝴蝶定理
蝴蝶定理 用面積法證明蝴蝶定理
用面積法證明蝴蝶定理 坎迪定理
坎迪定理 用面積法證明坎迪定理
用面積法證明坎迪定理 例題
例題 例題證明
例題證明(見右上圖)【PS:坎迪定理是蝴蝶定理的一般形式】 坎迪定理 (證明過程見右下圖) 用面積法證明坎迪定理 PS:共圓定理還可以證明蝴蝶定理和坎迪定理的一些推廣...
如果同一平面內的四個點在同一個圓上,則稱這四個點共圓,一般簡稱為“四點共圓”。四點共圓有三個性質:(1)共圓的四個點所連成同側共底的兩個三角形的...
等角共圓定理 若線段同側二點到線段兩端點連線夾角相等,那么這二點和線段二端點四點共圓。等角共圓定理是四點共圓的基本判定方法之一,可以看做是定理“等弧...
密克定理是幾何學中關於相交圓的定理。1838年,奧古斯特·密克(Auguste Miquel)敘述並證明了數條相關定理。許多有用的定理可由其推出。密克的第一條定理,是十八世紀...
哈格定理(Hagge theorem)關於點共圓的三個定理,設H是△ABC的垂心,P是任意點,連APBP、CP交⊙ABC於A’、B'、C’,命這三點分別關於BC、CA、AB的對稱點為A...
米奎爾定理(Miqule theorem)是關於米奎爾點的兩個定理:1.在△ABC的三邊BC,CA,AB所在直線上各任取一點X,Y,Z,則⊙AYZ,⊙BZX,⊙CXY三圓共點,交點Q稱為X,Y...
坎德定理是對圓內接四邊形構造射線、切線等操作後後對幾何及代數性質的研究,它與圓冪定理、根軸、調和點列聯繫密切,並且近年在高中數學聯賽及以上級別考試考察力度...
思路1:利用四點共圓來證明三圓共點。這是證明拿破崙定理的基礎。證明:設等邊△ABF的外接圓和等邊△ACD的外接圓相交於O;連AO、CO、BO。...
圓內接四邊形四頂點組成的四個三角形的內心、旁心共十六點,分配在八條直線上,每線上四點,而這八條線是互相垂直的兩組平行線,每組含四線,此為富爾曼定理。...
蝴蝶定理(Butterfly Theorem):設M為圓內弦PQ的中點,過M作弦AB和CD。設AD和BC各相交PQ於點X和Y,則M是XY的中點。蝴蝶定理的證明 該定理實際上是射影幾何中...
西姆森定理(Simsson theorem),亦譯為西姆松定理,是關於平面幾何中的點共線的兩個定理。表述為:過三角形外接圓上異於三角形頂點的任意一點作三邊或其延長線上的...
費爾巴哈定理描述了三角形的九點圓與其內切圓以及三個旁切圓的位置關係。是平面幾何學中十分優美的定理之一。...
圓外蝴蝶定理其實是一個沒有正式規定的定理,它是由蝴蝶定理衍生出的一個概念,且與蝴蝶定理有著相當大的聯繫,它的定義是這樣的:如圖,延長圓O中兩條弦AB與DC交...
薩蒙定理(Salmon theorem)又稱沙爾蒙定理,是關於點共線和距離成比例的兩個定理:1.自圓上一點引三弦.則以此三弦為直徑的圓的其它三個交點共線;2.圓心O至A、B...
球冪定理是圓冪定理的推廣,即空間形式。...... 又因為這兩條直線均與球O相交,所以Q、R、S、T四點共圓。然後就是圓冪定理的證明:(Q、R、S、T與下文中的...
請注意,所有四個圓都減少到點情況下,這正是托勒密定理。圖1.凱西定理 凱西定理證明 編輯 半徑為 的圓 與圓 相切於點 ,用符號 表示圓的中心,畢達哥拉斯定理...
