哈格定理

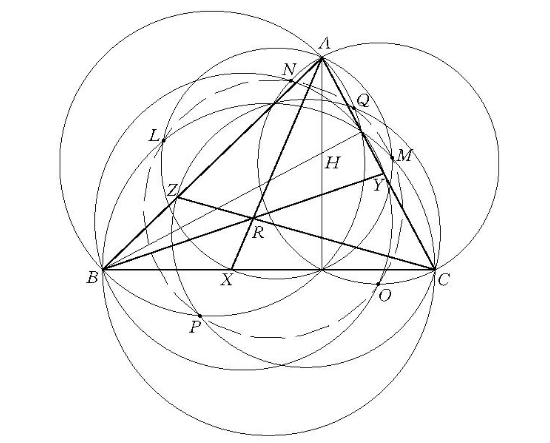
哈格定理(Hagge theorem)關於點共圓的三個定理，設H是△ABC的垂心，P是任意點，連APBP、CP交⊙ABC於A’、B'、C’，命這三點分別關於BC、CA、AB的對稱點為A₂、B₂、C₂，又連A₂P、B₂P、C₂P分別交AH、BH、CH於A₁、B₁、C₁，則A₁、B₁、C₁，A₂、B₂、C₂，H七點共圓。H是△ABC的垂心，X、Y、Z各是BC，CA、AB上的點，並假定AX，BY，CZ蘭線共點，若：(1)過H所引AX、BY、CZ的垂線各與直徑為BC、CA、AB的圓相交，則這些交點共圓；(2)過H所引AX，BY、CZ的垂線各與直徑為AX，BY、CZ的圓相交，則這些交點共圓；(3)直徑為BC、CA、AB的圓各與直徑為AX、BY、CZ的圓相交，則這些交點共圓或共線。

基本介紹

• 中文名：哈格定理
• 外文名：Hagge theorem
• 所屬學科：數學（平面幾何）
• 簡介：關於點共圓的三個定理

基本介紹

哈格定理是關於點共圓的三個定理：設H是△ABC的垂心；X，Y，Z分別是BC，CA，AB上的點，並假設AX，BY，CZ三線共點於R(如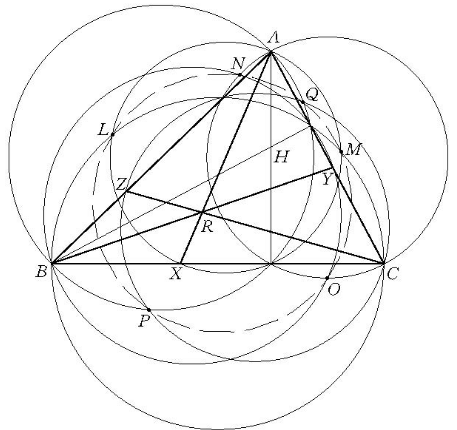圖1)。

圖1

1.若直徑為BC，CA，AB的圓分別與直徑為AX，BY，CZ的圓相交，則諸交點共圓或共線。如圖中以BC，AX為直徑的兩圓交於L，M兩點；以AC，BY為直徑的兩圓交於N，O兩點；以AB，CZ為直徑的兩圓交於P，Q兩點，則L，M，N，O，P，Q六點共圓。

2.過點H所引AX，BY，CZ的垂線分別與直徑為BC，CA，AB的圓相交，則諸交點共圓。

3.過點H所引AX，BY，CZ的垂線分別與直徑為AX，BY，CZ的圓相交，則諸交點共圓。

哈格定理的證明

設H是△ABC的垂心，P是任意點，聯結AP，BP，CP交⊙ABC於A'，B'，C'，命這三點分別關於BC，CA，AB的對稱點為A₂，B₂，C₂，又聯結A₂P，B₂P，C₂P分別交AH，BH，CH於A₁，B₁，C₁，求證：A₁，B₁，C₁，A₂，B₂，C₂，H七點共圓。

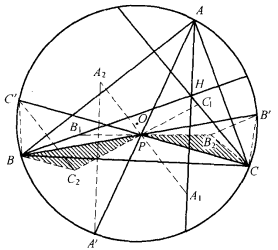圖2

證明 如圖，因為

又

所以

因為

有△PBC₂∽△PCB₂，所以

同理

又

從（1），（2），（3），（4），（5）可知：多邊形ABCA'B'C'與多邊形A₁B₁C₁A₂B₂C₂相似，因此且A₁B₁C₁A₂B₂C₂有外接圓。

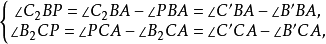
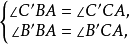
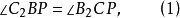
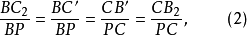
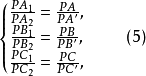
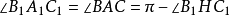
所以B₁，A₁，C₁，H四點共圓且A₁，B₁，C₁，A₂，B₂，C₂六點共圓，故A₁，B₁，C₁，A₂，B₂，C₂，H七點共圓。