西姆森定理

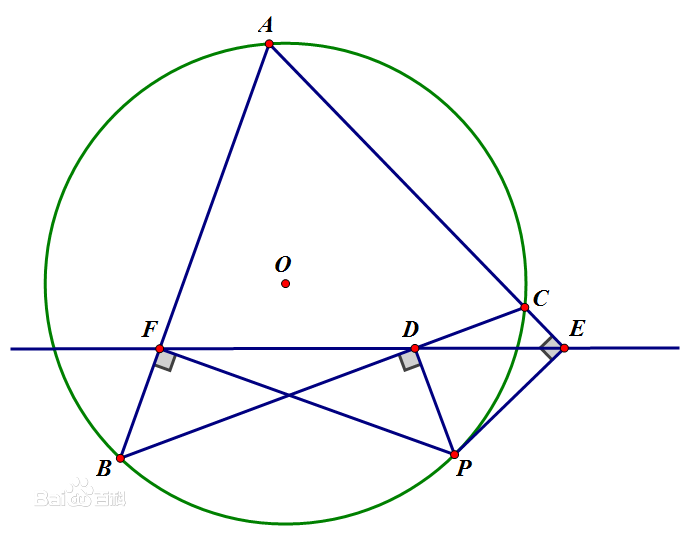
西姆森定理（Simsson theorem），亦譯為西姆松定理，是關於平面幾何中的點共線的兩個定理。表述為：過三角形外接圓上異於三角形頂點的任意一點作三邊或其延長線上的垂線，則三垂足共線，此線常稱為西姆松線或譯西摩松線（Simson line）。西姆森定理的逆定理為：若一點在三角形三邊所在直線上的射影共線，則該點在此三角形的外接圓上。

基本介紹

• 中文名：西姆森定理
• 外文名：Simsson theorem
• 別稱：西姆松定理
• 套用：平面幾何

定理內容

西姆松定理說明：有三角形 ，平面上有一點 。 在三角形三邊上的投影（即由 到邊上的垂足）共線（此線稱為西姆松線或譯西摩松線, Simson line）若且唯若 在三角形的外接圓上。

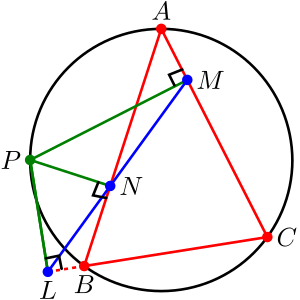圖1.西姆森定理說明圖

相關的結果有：

（1）稱三角形的垂心為 。西姆松線和 的交點為線段 的中點，且這點在九點圓上。

（2）兩點的西姆松線的交角等於該兩點的圓周角。

（3）若兩個三角形的外接圓相同，這外接圓上的一點 對應兩者的西姆松線的交角，跟 的位置無關。

證明

如圖1，若L、M、N三點共線，連結BP，CP，則因PL垂直於BC，PM垂直於AC，PN垂直於AB，有B、P、L、N和M、P、L、C分別四點共圓，有∠PBN = ∠PLN = ∠PLM = ∠PCM，故A、B、P、C四點共圓。

若A、B、P、C四點共圓，則∠PBN = ∠PCM。因PL垂直於BC，PM垂直於AC，PN垂直於AB，有B、P、L、N和M、P、L、C四點共圓，有∠PLN = ∠PBN = ∠PCM =∠PLM，故L、M、N三點共線。