一個數學史上的錯誤,就是將1797年瓦倫斯(William Wallace, 1768-1843) 的發現歸功於另一個數學家西摩松(Robert Simson, 1687-1768)。這個發現就是現在大家所熟知的西摩松線(Simson’s line)。
基本介紹
- 中文名:西摩松線
- 外文名:Simson’s line
- 領域:數學史
- 時間:1797
有關背景
定義
證明
一個數學史上的錯誤,就是將1797年瓦倫斯(William Wallace, 1768-1843) 的發現歸功於另一個數學家西摩松(Robert Simson, 1687-1768)。這個發現就是現在大家所熟知的西摩松線(Simson’s line)。

一個數學史上的錯誤,就是將1797年瓦倫斯(William Wallace, 1768-1843) 的發現歸功於另一個數學家西摩松(Robert Simson, 1687-1768)。這個發現就是現在大家所...
史坦納定理是幾何中的有名定理,其內容是:設△ABC的垂心為H,其外接圓上的任一點為P,△ABC關於點P的西摩松線通過線段PH的中點。...
波朗傑,設P、Q、R為△ABC的外接圓上的三點,若P、Q、R關於△ABC的西摩松線交於一點,則A、B、C三點關於△PQR的的西摩松線交於與前相同的一點...
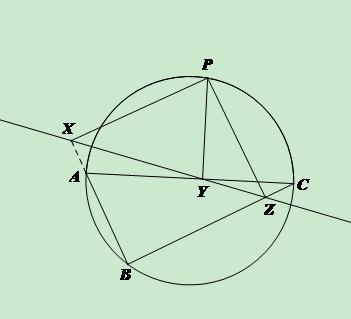
32.西摩松定理:從△ABC的外接圓上任意一點P向三邊BC、CA、AB或其延長線作垂線,設其垂足分別是D、E、R,則D、E、R共線,(這條直線叫西摩松線)...
而P,Q,R的西摩松線也都通過S,S是直線PQ,PR,QR中任一個的垂極點。一條直線的垂極點,關於這條線上所有點的垂足圓,有相同的冪 [1] 。...
32.西摩松定理:從△ABC的外接圓上任意一點P向三邊BC、CA、AB或其延長線作垂線,設其垂足分別是D、E、R,則D、E、R共線,(這條直線叫西摩松線)...
《近代的三角形幾何學》是平面歐氏幾何學的經典之作。以三線坐標和重心坐標為工具,對內接外切的三角形族、西摩松線、垂足三角形、垂極點、逆垂足三角形、三角形...
設P、Q、R為△ABC的外接圓上的三點,若P、Q、R關於△ABC的西摩松線交於一點,則A、B、C三點關於△PQR的的西摩松線交於與前相同的一點...
