鏡像線出現在關於幾個點共線的問題中。△ABC的外接圓上的點P關於邊BC,CA,AB的對稱點X,Y,Z和△ABC的垂心H在同一條直線上,這條直線稱為點是關於△ABC的鏡像線。
基本介紹
- 中文名:鏡像線
- 外文名:mirrorimage line
- 適用範圍:數理科學
簡介
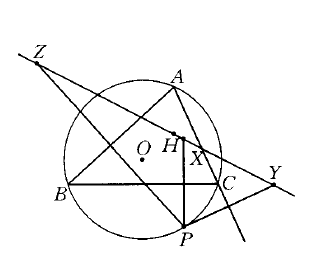 圖1
圖1出處
證明
 圖2
圖2鏡像線出現在關於幾個點共線的問題中。△ABC的外接圓上的點P關於邊BC,CA,AB的對稱點X,Y,Z和△ABC的垂心H在同一條直線上,這條直線稱為點是關於△ABC的鏡像線。
 圖1
圖1 圖2
圖2鏡像線出現在關於幾個點共線的問題中。△ABC的外接圓上的點P關於邊BC,CA,AB的對稱點X,Y,Z和△ABC的垂心H在同一條直線上,這條直線稱為點是關於△ABC的鏡像...
鏡像站點是將網站的多個副本放置不同的伺服器,這樣可能提高反應速度,用戶可以在訪問較少或相對速度較快的伺服器上取得信息,提高了網路傳輸效率,也提高了網站的安全...
鏡像伺服器(Mirror server)與主伺服器的服務內容都是一樣的,只是放在一個不同的地方,分擔主機的負載。簡單來說就是和照鏡子似的,能看,但不是原版的。在網上...
鏡像法是直接建立在唯一性定理基礎上的一種求解靜電場問題的方法。適用於解決導體或介質邊界前存在點源或線源的一些特殊問題。鏡像法的特點是不直接求解電位函式所...
鏡像原理是指位於無窮大的、理想導電平板上方空間的任何電荷產生的磁場,在電氣上等效於原來的電荷產生的電場疊加上由它的鏡像產生的電場。當一個聲源靠近剛性壁面時...
鏡像式行銷針對於傳統行銷模式的新型行銷模式的概括性描述。“鏡像式”並非是某一種特殊的行銷方式,而是偏重於概括處於21世紀網際網路商業模式時代的多元化、多層次、...
集群技術的一種。是將建立在同一個區域網路之上的兩台伺服器通過軟體或其他特殊的網路設備,將兩台伺服器的硬碟做鏡像。其中,一台伺服器被指定為主伺服器,另一台...
青年實力作家陳新長篇小說《鏡像》,由江西教育出版社常規出版。該書26萬字,首印2萬冊,風格溫馨、大氣,活潑又不失穩重。該小說是一部反傳統的長篇小說,其令人驚詫...
鏡像指示位,緩衝區的長度如果是n,邏輯地址空間則為0至n-1;那么,規定n至2n-1為鏡像邏輯地址空間。...
《鏡像追蹤》由北京北角奇戈影視傳媒、湖南藍色暢想教育圖書出品,由代藝霖執導、張赫、田家達、郭野、葛秦宏、胡嘉欣、王藝曈、黛安娜、柳伊等主演的科幻懸疑網劇。...
鏡像,原意是光學裡指的物體在鏡面中所成之像。引用到電腦網路上,一個網站的鏡像是指對一個網站內容的拷貝。鏡像通常用於為相同信息內容提供不同的源,特別是在...
鏡像頻率干擾是超外差接收機特有的現象,設信號頻率為fs,振盪頻率為fc,中頻fid=fc-fs, 在比fs高二個fid處就有一個頻率fm,,它像是以fc為鏡子,站在fs處看到...
鏡像阿拉德,是網路遊戲《地下城與勇士》中的一處副本。DNF在2014年6月開啟“創新世紀”版本(俗稱大轉移),所有大轉移之前阿拉德大陸的所有除遠古的副本(血蝴蝶之舞...
鏡像相似(mirror image similar)亦稱逆相似或異向相似,是一種特殊相似形。一個平面到自身的變換,如果對於任意兩點A,B,以及對應點A',B',總有A'B'=k.AB(k為...
鏡像大師(Mirror Master)是美國DC漫畫旗下超級反派,初次登場於《閃電俠》(Flash)第105期(1959年3月)。本名塞繆爾·約瑟夫·“薩姆”·斯卡德(Samuel Joseph “Sam...
這兩個電台信號與本機振盪頻率各相差465KHz,如同“鏡像”一樣。鏡像抑制就是在接收630KHz時,對1560KHz信號的制抑制能力,或在接收1560KHz信號時對630KHz信號的抑制...
變形金剛——Shattered Glass, 被譯為玻璃渣/鏡像宇宙/大跌眼鏡/破碎玻璃/黑白顛倒/逆轉TF, 是2008年BOTCON限定主題平行宇宙設定, 主線故事隸屬於TF時間線(TIMELINE...
《鏡像東方》是2009年巴蜀書社出版的圖書,作者是高力、任曉楠。...... 本書論及的“鏡像”並非涉及當代法國著名的精神分析學家拉康在1936年顛覆弗洛伊德的精神分析...
鏡像象棋 基本規則同象棋,不同規則如圖文: 1、棋盤縱向擴展增加"鏡像"部分,雙方各有三個士、象和正反兩面九宮。 2、雙方原底線外的地域為"鏡像區",只是擴展無...
鏡像怪物一款策略小遊戲,遊戲大小為1.39 MB。...... 鏡像怪物一款策略小遊戲,遊戲大小為1.39 MB。...滑鼠控制,點擊並拖動滑鼠畫出白色對稱軸線,巫師就能跳...
