基本介紹
- 中文名:圓外蝴蝶定理
- 套用:求解數學問題
- 特點:由蝴蝶定理衍生出的一個概念
- 性質:數學定理
定理介紹,衍生原理,相同點,對比證明,擴展,套用,
定理介紹
衍生原理
如圖,左邊的是圓內蝴蝶定理,右邊的是圓外蝴蝶定理,我們可以推理,一條直線L進過圓O內部,過O且垂直於直線L的直線h,P為垂足,圓內兩條弦AB、CD交於P,CB與AD所在直線交直線L於M、N,CA和BD所在直線交直線L於E、F,當直線L以垂線h方向向圓外移動,至直線L不與圓相交時,垂足兼交點的P移動到圓外,就形成了右邊的圓外蝴蝶定理,且得出的結論與圓內蝴蝶定理完全一樣:PM=PN,PE=PF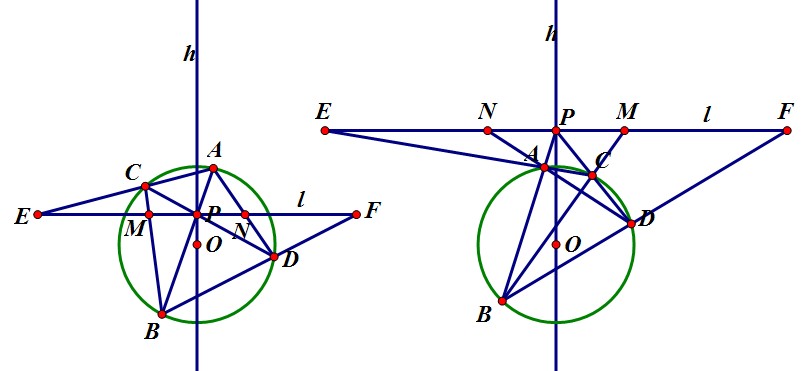 衍生原理
衍生原理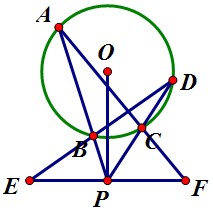 圓外蝴蝶定理
圓外蝴蝶定理
 衍生原理
衍生原理 圓外蝴蝶定理
圓外蝴蝶定理相同點
同樣擁有蝴蝶一樣的形狀,在解法上,幾乎一模一樣,目前解決圓外蝴蝶定理的正向證明有很多,其中在蝴蝶定理與圓外蝴蝶定理通用的解法有:過圓心做垂直,利用垂弦定理,相似三角形,四點共圓,全等;另外一種則是不用圓心,直接做平行,導圓周角,四點共圓。而在解決逆向證明的時候,前者沒有“對偶解法”則會失效,而後者的“對偶解法”——做對稱三角形,則與做平行線成了兩種解決一切圓有關的蝴蝶定理正、逆向證明以及其擴展形式的通用對偶解法。
對比證明
正向證明——做平行線
如圖(1)圓內蝴蝶定理的證明,已知P為弦EF中點,求證PM=PN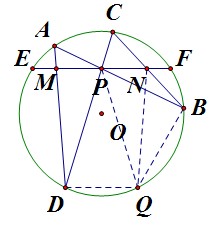 (1)
(1)
 (1)
(1)解:輔助線:過D點做MN的平行線,交圓O於Q,連線PQ,QN,BQ
∵DQ∥MN,P為EF中點
∴易證PD=PQ
∴∠PDQ=∠QPN
又∵∠CDQ+∠CBQ=180°
∴∠NPQ+∠NBQ=180°
∴P、N、B、Q四點共圓
∴∠CBA=∠NQP=∠MDP
∵∠MPD=∠NPQ,PD=PQ,∠PDM=∠PQN
∴△PDM≌△PQN(ASA)
∴PM=PN
如圖(2)圓外蝴蝶定理的證明,已知OP⊥MN,求證PN=PM
解:輔助線:如(1)所述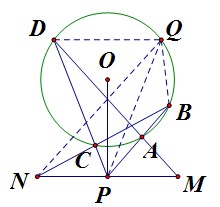 (2)
(2)
 (2)
(2)∵DQ∥MN,OP⊥MN
∴易證PD=PQ ∠NQP=∠MDP ∠DPO=∠QPO(根據圓的對稱性)
∴∠PDQ=∠QPM ∠MPD=∠NPQ
又∵∠CDQ+∠CBQ=180°
∴∠MPQ+∠NBQ=180°
∴P、N、Q、B四點共圓
∴∠CBA=∠NQP=∠MDP
∵∠MPD=∠NPQ,PD=PQ,∠PDM=∠PQN
∴△PDM≌△PQN(ASA)
∴PM=PN
逆向證明——做對稱三角形
如圖(3)圓內蝴蝶定理的逆向證明,已知PM=PN,求證P為EF中點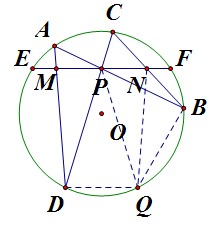 (3)
(3)
 (3)
(3)解:輔助線:做△PMD關於MN中垂線對稱的△PNQ,連線DQ,BQ
∵△PMD與△PNQ對稱
∴△PMD≌△PNQ
∴∠ADC=∠PQN=∠ABC
∴P、N、B、Q四點共圓
∴∠NPQ+∠NBQ=180°
∵PD=PQ,DQ∥MN
∴∠NPQ=∠CDQ
∴∠CDQ+∠CBQ=180°
∴Q在圓O上
∴易證OP⊥DQ
∴OP⊥EF
∴P為EF中點
如圖(4)圓外蝴蝶定理的逆向證明,已知PM=PN,求證PO⊥MN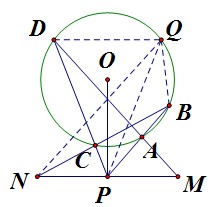 (4)
(4)
 (4)
(4)解:輔助線:如(3)所述
∵△PMD與△PNQ對稱
∴△PMD≌△PNQ
∴∠ADC=∠PQN=∠ABC
∴P、N、B、Q四點共圓
∴∠MPQ+∠NBQ=180°
∵PD=PQ,DQ∥MN
∴∠MPQ=∠CDQ
∴∠CDQ+∠CBQ=180°
∴Q在圓O上
∴易證OP⊥DQ
∴OP⊥MN
擴展
如圖,弦DC與BA延長交於圓外一點P,延長弦DB與AC,與過P點的OP的垂線分別交於N、M,求證PM=PN(正向證明)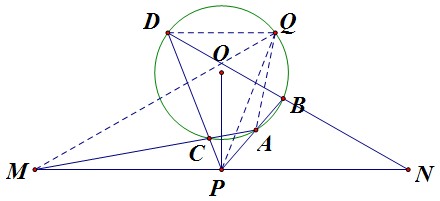 擴展形式(正向證明)
擴展形式(正向證明)
 擴展形式(正向證明)
擴展形式(正向證明)解:輔助線:過D點做MN平行線,交圓O於Q,連線MQ,PQ,AQ
∵OP⊥MN,DQ∥MN
∴OP⊥DQ
∴PD=PQ
∴∠PDQ=∠QPN
∵∠PDQ+∠CAQ=180°
∴∠QPN+∠MAQ=180°
∴P、M、Q、A四點共圓
∴∠MQP=∠MAP=∠NDP
∵∠QPM=∠DPN,PQ=PD,∠MQP=∠NDP
∴△MPQ≌△NPD(ASA)
∴PM=PN
如圖,弦DC與BA延長交於圓外一點P,延長弦DB與AC,與過P點的直線分別交於N、M,若PM=PN,求證OP⊥MN(逆向證明)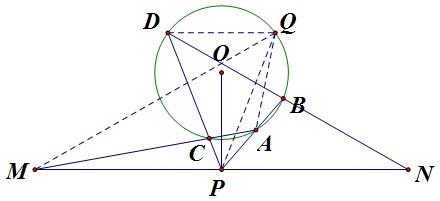 擴展形式(逆向證明)
擴展形式(逆向證明)
 擴展形式(逆向證明)
擴展形式(逆向證明)解:輔助線:做△PDN關於MN中垂線對稱的△PQM,連線DQ,AQ
∵△PDN與△PQM對稱
∴△PDN≌△PQM
∴∠PDB=∠PAC=∠MQP
∴P、M、Q、A四點共圓
∴∠QPN+∠MAQ=180°
∵PD=PQ,DQ∥MN
∴∠QPN=∠PDQ
∴∠PDQ+∠CAQ=180°
∴Q在圓O上
∴易證OP⊥DQ
∴OP⊥MN
套用
解:輔助線:做出△ABC的外接圓圓O,圓O與CH交於F,連線BH,連線BF並延長與ED延長線交於G
∵H為△ACB的垂心
∴BA⊥CH,CA⊥BH
∴∠DBH=∠DCA=∠DBF
∵∠FDB=∠HDB,BD=BD,∠DBF=∠DBH
∴△DBF≌△DBH(ASA)
∴DF=DH
∵BF與CA的延長線交OD垂線於G、E
∴DG=DE(圓外蝴蝶定理)
∵DF=DH,∠FDG=∠HDE,DG=DE
∴△FDG≌△HDE(SAS)
∴∠GFD=∠CFB=∠CAB=∠DHE
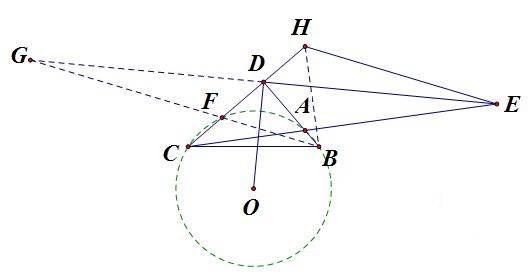 輔助線套用
輔助線套用