富爾曼定理

圓內接四邊形四頂點組成的四個三角形的內心、旁心共十六點，分配在八條直線上，每線上四點，而這八條線是互相垂直的兩組平行線，每組含四線，此為富爾曼定理。

基本介紹

• 中文名：富爾曼定理
• 外文名：Fuhrmann theorem
• 所屬學科：數學（平面幾何）
• 相關概念：內心，旁心等

基本介紹

富爾曼定理(Fuhrmann theorem)是關於三角形的若干特殊點的共線與共圓的兩個定理，第一個是關於圓上四點所成三角形內心與旁心分布狀態定理；第二個是關於與三角形垂心、內心(或旁心)有關的八點共圓問題。

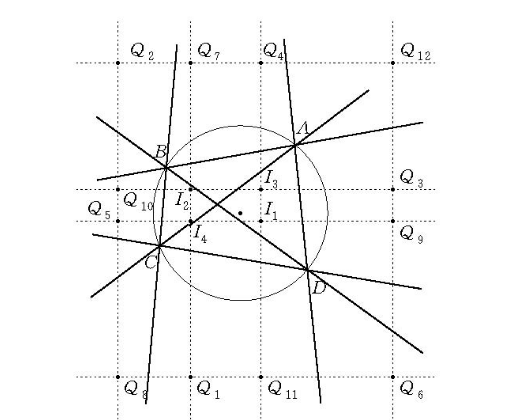
圓上四點所成三角形內心與旁心分布定理

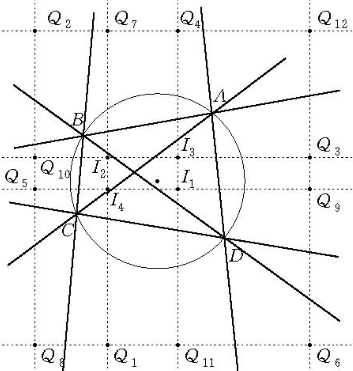一是關於圓上四點所成三角形內心與旁心分布狀態定理。圓上四點兩兩連成四個三角形，它們的內心、旁心合計十六點分配在八條直線上，每線上四點，而這八線是兩組互相垂直的平行線，每組含四線(如圖1)。

圖1

八點共圓問題

二是關於與三角形垂心、內心(或旁心)有關的八點共圓問題，在△ABC中，H是垂心，I是內心或旁心，N是對應的“納格爾點”；連結AI，BI，CI交⊙ABC於點A′，B′，C′，命這三點分別關於BC，CA，AB的對稱點為A₂，B₂，C₂；引NA₁⊥AH，NB₁⊥BH，NC₁⊥CH，垂足為A₁，B₁，C₁，則A₁，B₁，C₁，A₂，B₂，C₂，H，N八點共圓(如圖2)。

圖2（放大圖為圖3）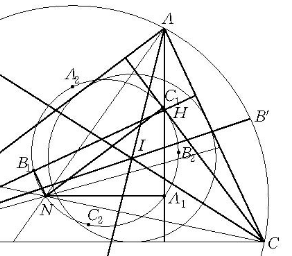

圖3 (圖2放大部分圖)