等角共軛

幾何學中，設點P是三角形ABC平面上一點，作直線PA、PB和PC分別關於角A 、B和C的平分線的反射，這三條反射線必然交於一點[1]，稱此點為P關於三角形ABC的等角共軛。 （這個定義只對點，不是對三角形ABC的邊。）點P的等角共軛點經常記作P*，顯然P*的等角共軛點即為P。

基本介紹

• 中文名：等角共軛
• 領域：幾何學
• 屬性：專業術語
• 解釋：《圓錐曲線的幾何性質》

含義

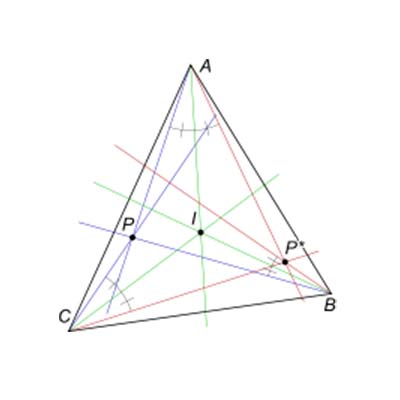
內心I的等角共軛點是自身。垂心H的等角共軛點是外心O。重心的等角共軛點是類似重心K。在三線坐標中，如果X = x : y : z是不在三角形ABC邊上的一點，那么它的等角共軛是1/x : 1/y : 1/z。因此，X的等角共軛有時也記作X −1。三角形內部的點集S在三線乘法

等角共軛

(p : q : r) * (u : v : w) = pu : qv : rw，

下構成一個交換群。 S中任何一點X的逆是X −1。

因為等角共軛是一個函式，從而我們可以討論一個點集的等角共軛。譬如，直線的等角共軛是一條外接圓錐曲線；確切的，若直線交外接圓於0、1或2 點，其等角共軛分別為橢圓、拋物線或雙曲線。外接圓的等角共軛是無窮遠直線。一些有名的三次曲線（例如：Thompson三次曲線、Darboux三次曲線、Neuberg三次曲線）是自等角共軛的，即如果X位於這些三次曲線上，那么X −1也在其上。

定理

1.等角點的一個常用性質（Poncelet定理）：

“設E、F是∠APB內的兩點，滿足∠APF=∠BPE。作E、F關於PA、PB的軸對稱點S、T．求證：FS=ET．”

Poncelet定理等價表述為：

“∠APB內的一對等角點E、F（即滿足∠APF=∠BPE），關於PA、PB兩邊的光路反射路徑長度一定相等！”

2.“角內兩點形成等角關係的另一充要條件是，它們在兩邊上的四個射影共圓！ 所共圓圓心即為這組等角點的中點．”

圓錐曲線套用

由橢圓外一點P引橢圓的兩條切線PE、PF，則橢圓的兩焦點為∠EPF內的一對等角點．

1.等角共軛解決《圓錐曲線的幾何性質》問題282

2.較複雜的等角共軛問題，暫時沒想出來思路（《圓錐曲線的幾何性質》問題196、43）

3 .四點共圓中的結論，找不到思路（《圓錐曲線的幾何性質》問題289）