基本介紹
- 中文名:三角形外角定理
- 外文名:exterior angle theorem of a triangle
- 所屬學科:數學
- 所屬問題:平面幾何(三角形)
基本介紹
 圖1
圖1三角形外角定理的證明
證法一
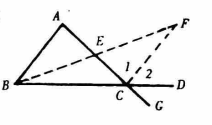 圖2
圖2證法二
推論及證明
證法一
證法二
證法三
 圖3
圖3
 圖4
圖4
 圖1
圖1 圖2
圖2 圖3
圖3
 圖4
圖4三角形外角定理(exterior angle theorem of a triangle)是平面幾何的重要定理之一,指三角形的一個外角等於與它不相鄰的兩個內角的和。由此可得:三角形的外角大於...
三角形的一條邊與另一條邊的延長線組成的角,叫做三角形的外角。外角的個數等於多邊形邊數的兩倍。三角形外角和是360°(多邊形的外角和一般是每個頂點只取一個...
三角形內角和等於180度;一個外角大於與它不相鄰的任一個內角,等於與它不相鄰的兩個內角和,多邊形的外角和為360度,外角越多,越接近圓。...
三角形的重心,外心,垂心,內心和旁心稱之為三角形的五心。三角形五心定理是指三角形重心定理,外心定理,垂心定理,內心定理,旁心定理的總稱...
圓周角定理指的是一條弧所對圓周角等於它所對圓心角的一半。這一定理叫做圓周...∠COD=∠CAD+∠ACO=2∠CAD(三角形的外角等於兩個不相鄰兩個內角的和)...
任意正多邊形的外角和=360°正多邊形任意兩條相鄰邊連線所構成的三角形是等腰三角形多邊形的內角和定義〔n-2〕×180°多邊形內角和定理證明...
旁心定理性質 編輯 1、三角形一內角平分線和另外兩頂點處的外角平分線交於一點,該點即為三角形的旁心。2、每個三角形都有三個旁心。...
P是圓外一點,由P作圓的兩條割線PAC、PBD,稱∠P為圓外角。圓外角度數定理:...則由三角形外角公式:∠P=∠BAD-∠D=1/2(弧BD的度數-弧AC的度數)...
由定義可知,三角形的內角平分線是一條線段。三角形有六個外角,所以三角形有六條外角平分線。把一個角平均分成兩個角的線段或射線叫做這個角的平分線。...
(1) 三角形三邊的關係:三角形的任意兩邊之和大於第三邊,兩邊之差小於第三邊。(2) 三角形內角和定理: 。(3) 三角形的任意一個外角等於與它不相鄰的兩個...
定理:設三角形重心為O,BC邊中點為D,則有AO = 2 OD。重心坐標為三頂點坐標...三角形的一條內角平分線與其他兩個角的外角平分線交於一點,即三角形的旁心。...
三角形是由同一平面內不在同一直線上的三條線段‘首尾’順次連線所組成的封閉圖形,在數學、建築學有套用。常見的三角形按邊分有普通三角形(三條邊都不相等),...
