基本介紹
- 中文名:第三類貝塞爾函式
- 外文名:Bessel function of the third kind
- 別名:漢克爾函式
- 定義:貝塞爾方程的線性無關解
- 一級學科:數學
- 二級學科:特殊函式
- 類型:數學名詞
歷史
現實背景和套用範圍
第三類貝塞爾函式
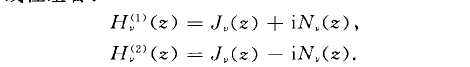







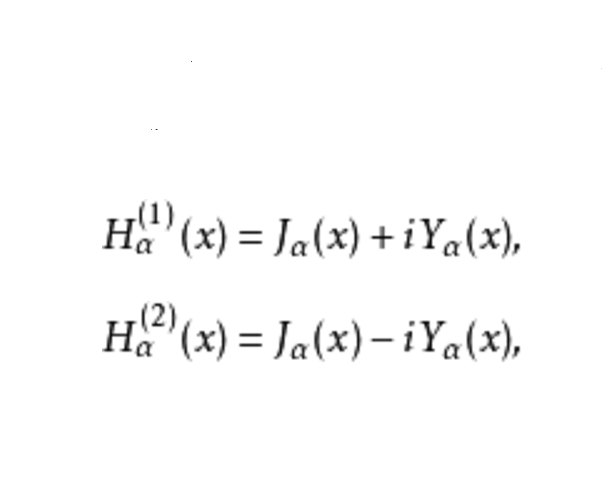
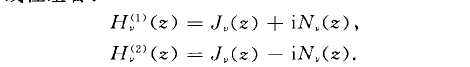







第三類貝塞爾函式(Bessel function of the third kind)亦稱漢克爾函式,貝塞爾方程的線性無關解,可以表示為第一類和第二類貝塞爾函式的線性組合,它們在除去負實軸 (-∞,0) 的z平面上單值解...
不能由第一類貝塞爾函式的簡單組合得到,此時需要通過一個求極限過程來計算函式值。第三類貝塞爾函式(亦稱漢克爾函式)定義為 ,其中 為虛數,用n階(正或負)貝塞爾函式可解稱為貝塞爾方程的微分方程。套用範圍 貝塞爾方程是在柱坐標或球坐標下使用分離變數法求解拉普拉斯方程和亥姆霍茲方程時得到的(在圓柱域問題中得...
變形第三類貝塞爾函式 變形第三類貝塞爾函式(modified Bessel function of the third kind)是1993年發布的數學名詞。公布時間 1993年經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
§5.1 貝塞爾方程的引出 §5.2 貝塞爾方程的求解 §5.3 當n為整數時貝塞爾方程的通解 §5.4 貝塞爾函式的遞推公式 §5.5 函式展開成貝塞爾函式的級數 5.5.1 貝塞爾函式的零點 5.5.2 貝塞爾函式的正交性 §5.6 貝塞爾函式套用舉例 §5.7 貝塞爾函式的其他類型 5.7.1 第三類貝塞爾函式 5....
第五章 貝塞爾函式 5.1 貝塞爾方程的引出 5.2 貝塞爾方程的求解 5.3 當n為整數時貝塞爾方程的通解 5.4 貝塞爾函式的遞推公式 5.5 函式展成貝塞爾函式的級數 5.5.1 貝塞爾函式的零點 5.5.2 貝塞爾函式的正交性 5.6 貝塞爾函式套用舉例 5.7 貝塞爾函式的其他類型 5.7.1 第三類貝塞爾函式 5.7.2 虛...
第二類貝塞爾函式(Bessel function of the second kind ),亦稱諾伊曼函式(Neumann function),為貝塞爾方程的第二解,與第一類貝塞爾函式線性無關,且可由第一類貝塞爾函式的定義在除去負實軸(-∞,0)的z平面上單值解析。歷史 貝塞爾函式的幾個正整數階特例早在18世紀中葉就由瑞士數學家丹尼爾·伯努利在研究懸鏈振動...
5.2.2 調和函式的積分表達式 5.2.3 調和函式的性質 5.3 格林函式 5.3.1 格林函式的引入 5.3.2 格林函式的性質 5.4 兩種特殊區域的格林函式及拉普拉斯方程的第一邊值問題的解 5.4.1 上半空間的格林函式 5.4.2 球形區域內的格林函式 小結 中英文辭彙對照 習題5 第6章 貝塞爾函式 6.1 貝塞爾方程...
變形第二類貝塞爾函式 變形第二類貝塞爾函式(modified Bessel function of the second kind)是1993年發布的數學名詞。公布時間 1993年經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
變形第一類貝塞爾函式 變形第一類貝塞爾函式(modified Bessel function of the first kind)是1993年公布的數學名詞。公布時間 1993年經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
阿龍扎楊-史密斯核(Aronszajn-Smith kernel)是一種位勢核。其中0<α<+∞,Kλ表示第三類修正貝塞爾函式。中文名 阿龍扎楊-史密斯核 外文名 Aronszajn-Smith kernel 適用範圍 數理科學 目錄 1 簡介 2 核 3 貝塞爾函式 阿龍扎楊-史密斯核簡介 編輯 播報 阿龍扎楊-史密斯核是一種位勢核。 [1] ...
5.5.2第三類貝塞爾函式 5.5.3虛宗量的貝塞爾函式 5.5.4半奇貝塞爾函式 5.5.5球貝塞爾函式 5.5.6變形貝塞爾函式 5.6柱函式在定解問題中的套用 習題5 第6章球坐標下的分離變數法(球函式)6.1球坐標下的分離變數法 6.1.1球坐標下Δu=0的分離變數法 6.1.2球坐標下的Δu+λu=0分離變數 6.2勒...
4.5.1 第三類貝塞爾函式 4.5.2 球貝塞爾函式 4.6 虛變數(或變形)貝塞爾函式 4.6.1 第一類和第二類變形的貝塞爾函式 4.6.2 整數階變形貝塞爾函式 4.6.3 半奇數階變形貝塞爾函式 4.7 變數為實數的貝塞爾函式 4.7.1 貝塞爾方程的特徵值問題 4.7.2 特徵函式族的性質 4.7.3 球貝塞爾方程的特徵值...
漢克爾著名的貢獻包括他提出的貝塞爾方程的一類特殊函式解(稱為“第三類貝塞爾函式”或漢克爾函式)和線性代數中的漢克爾矩陣。同時,他還是著名的數學史專家,主要著作有《近幾世紀數學的發展》(Entwicklung der Mathematik in den letzten Jahrhunderten,1869)《古代與中世紀數學史》(Zur Geschichte derMathematik in ...
4.5.2 連帶勒讓德函式的性質 4.5.3 連帶勒讓德函式在解數理方程中的套用 4.6 球函式 4.6.1 一般的球函式定義 4.6.2 球函式的正交歸一性 4.6.3 球函式的套用 4.7 貝塞爾函式 4.7.1 三類貝塞爾函式(貝塞爾方程的解)4.7.2 貝塞爾方程的本徵值問題 4.8 貝塞爾函式的性質 4.8.1 貝塞爾函式...
第三節 超幾何函式 一、超幾何級數與超幾何函式 二、超幾何函式的積分表達式 三、鄰次函式和遞推關係式 四、變換公式 五、可用超幾何函式表示的初等函式 六、超幾何函式的計算 第四節 貝塞爾函式 一、貝塞爾函式與貝塞爾方程 二、第一類貝塞爾函式 三、第二類貝塞爾函式 四、第三類貝塞爾函式 五、變型(或虛宗量...
9.4.2連帶勒讓德函式的微分表達式 9.4.3連帶勒讓德函式的母函式 9.4.4連帶勒讓德函式的遞推公式 9.4.5連帶勒讓德函式的正交歸一性 9.4.6連帶勒讓德函式的廣義傅立葉級數展開 習題9 第10章貝塞爾函式 10.1貝塞爾函式的定義 10.1.1貝塞爾方程的級數解 10.1.2三類貝塞爾函式 10.2貝塞爾函式的性質 1...
6.4.2 貝塞爾函式的模 233 6.5 柱坐標下的邊值問題 236 6.5.1 柱對稱的邊值問題 236 6.5.2 二重傅立葉G貝塞爾級數的邊值問題 240 6.6 虛宗量貝塞爾函式 243 6.6.1 修正的貝塞爾函式 243 6.6.2 修正的貝塞爾函式邊值問題 246 6.7 其他類型的貝塞爾函式 248 6.7.1 第三類貝塞爾函式與...
4.6.1 一般的球函式定義 122 4.6.2 球函式的正交歸一性 122 4.6.3 球函式的套用 123 4.7 貝塞爾函式 125 4.7.1 三類貝塞爾函式(貝塞爾方程的解) 125 4.7.2 貝塞爾方程的本徵值問題 128 4.8 貝塞爾函式的性質 129 4.8.1 貝塞爾函式的母函...
《21世紀高等院校教材·數學物理方程及其套用》主要內容包括:數學模型——定解問題,分離變數法,特徵值問題,貝塞爾函式,勒讓德多項式,積分變換法,波動方程的達朗貝爾法,格林函式法,運算元級數法和數學物理方程在工程技術中的套用。全書以解題方法為主線編排章節,在建立三類典型方程的各種定解問題的基礎上,對各類定...
11.5.5 【實例64】 貝塞爾函式求值 476 11.5.6 【實例65】 變型貝塞爾函式求值 477 11.6 Carlson橢圓積分 479 11.6.1 [算法113] 第一類橢圓積分 479 11.6.2 [算法114] 第一類橢圓積分的退化形式 481 11.6.3 [算法115] 第二類橢圓積分 483 11.6.4 [算法116] 第三類橢圓積分 486...
7.7 振動圓形膜和貝塞爾函式295 7.7.1 概述295 7.7.2 分離變數296 7.7.3 特徵值問題(一維情形)297 7.7.4 貝塞爾微分方程299 7.7.5 奇異點和貝塞爾微分方程299 7.7.6 貝塞爾函式及其漸近性質(在z=0附近)301 7.7.7 涉及貝塞爾函式的特徵值問題302 7.7.8 振動圓形膜的初值問題304 7.7...
《數學物理方法》是2014年由高等教育出版社出版的教材,作者是臧濤成、馬春蘭、潘濤。該書可作為高等學校物理類專業的教材或參考書,亦可作其他專業讀者的輔助參考書。全書由復變函式論和數學物理方程兩部分組成,以常見物理問題中三類偏微分方程定解問題的建立和求解為中心內容。成書過程 《數學物理方法》是作者結合十...
