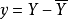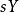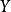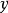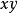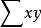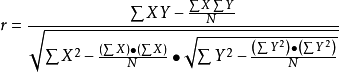積差相關是英國統計學家皮爾遜於20世紀初提出的一種計算相關的方法，因而被稱為皮爾遜積差相關，簡稱皮爾遜相關。積差相關又稱為積矩相關（product-moment coefficient of correlation)。通常，人們把離均差乘方之和除以N，用“積矩”概念表示。積差相關是一種運用較為普遍的計算相關係數的方法，也是揭示兩個變數線性相關方向和程度最常用和最基本的方法。
基本介紹
- 中文名：皮爾遜相關
- 外文名：product-moment coefficient of correlation
- 別稱：皮爾遜積差相關，積差相關
- 提出者： 皮爾遜
- 提出時間：20世紀初
- 套用學科：心理學
- 適用領域範圍：統計學
- 適用領域範圍：統計學
（一）運用標準差與離均差的計算公式
式中：
為兩個變數的離均差，
,
;
根據 
推導，公式又可以改寫成:
通常把公式中的
稱為協方差（covariance)。所謂協方差就是兩個變數離均差乘積的平均數，用公式表示為
。兩列變數離均差的乘積
的大小，能夠反映兩列變數的一致性。即當
大
也大時，
也大；當
小
也小時，
也小。
的絕對值大小隨
兩列變數的一致性程度而變。
的絕對值越大，表示
與
之間的線性關係越強，即這些點越接近一直線。
如果直接運用原始數據計算皮爾遜積差相關係數，可推演出以下公式：
