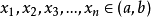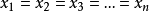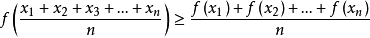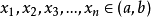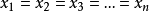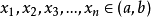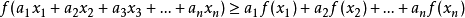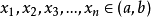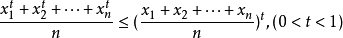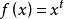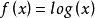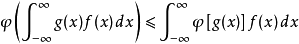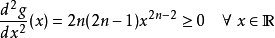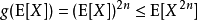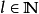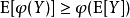琴生不等式

琴生不等式以丹麥技術大學數學家約翰·延森（Johan Jensen）命名。它給出積分的凸函式值和凸函式的積分值間的關係。

琴生（Jensen）不等式（也稱為詹森不等式），使用時注意前提、等號成立條件。

基本介紹

• 中文名：琴生不等式
• 外文名：Jensen Inequality
• 別稱：詹森不等式
• 注意：注意前提、等號成立條件
• 發明人：琴生
• 適用學科：高等數學

概述

1.若 是區間 上的凸函式，則對任意的 ，有不等式:

有若且唯若 時等號成立。

2.若 是區間 上的凹函式，則對任意的 ，有不等式:

若且唯若 時等號成立。

3.其加權形式為：

若 是區間 上的凸函式，則對任意的 ，且 ，

有

若 是區間 上的凹函式，則對任意的 ，且 ，

則有f（a1x1+a2x2+a3x3.....+anxn）≤a1f(x1)+a2f(x2)+a3f(x3).....+anf（xn）

套用

有了這個結論以後，使用琴生不等式就非常方便了，

如今我們可以非常容易的證明一般情況的平均不等式

比如

i).

ii).

iii).

其中前面兩個取就可以了

後面一個取就可以了。

舉一個簡單的例子：在中為凸函式（國外教材定義；若為凹函式，則國內教材定義），如圖所示：

同時，值得注意的是，上凸、下凸、凹、凸的含義是不同的。如圖：

涉及機率密度函式的形式

假設Ω是實線的可測子集，f（x）是一個非負函式

在機率語言中，f是機率密度函式。

然後Jensen的不等式變成了關於凸積分的下面的陳述：

如果g是任何實值可測函式且φ在g的範圍內是凸的，那么：

如果g（x）=x，那么這種不等式的形式可以簡化為一個常用的特例：

例如：隨機變數的偶數矩

如果g（x）=x，並且X是一個隨機變數，那么g是凸的

所以

特別是，如果有的甚至瞬間2N的X是有限的，X具有有限的均值。這個論證的延伸表明X具有每個階的有限矩劃分ñ。

替代有限形式

令Ω= {x₁，...x_n}，並且以μ為Ω上的計數度量，則一般形式簡化為關於和的聲明：

，

條件是λi≥0和

還有一個無限的離散形式。

統計物理學

當凸函式是指數函式時，Jensen不等式在統計物理學中特別重要，給出：

，

其中期望值是關於隨機變數X中的一些機率分布。

這種情況下的證明非常簡單（參見Chandler，第5.5節）。理想的不平等直接來自書寫

• {\ displaystyle \ operatorname {E} \ left [e ^ {X} \ rightname = {E ^ {\ operatorname {E} [X]} \ operatorname {E} \ [X]} \右]}

然後套用不等式ë≥1 +X至最終指數。

資訊理論

如果p（X）是用於真正的機率分布X和q（X）是另一種分布，然後施加Jensen不等式隨機變數ÿ（X）=q（X）/p（X）和函式φ（ÿ）= -log（y）給出

因此：

一個稱為吉布斯不平等的結果。

它表明，當代碼是基於真實機率p而不是任何其他分布q分配時，平均訊息長度被最小化。即非負的量被稱為相對熵的q從p。

由於-log（X）為嚴格凸函式X> 0，它遵循：當等號成立p（X）等於q（X）幾乎無處不在。

Rao-Blackwell定理

主要文章：Rao-Blackwell定理

如果L是一個凸函式，一個亞西格瑪代數，然後，從Jensen不等式的條件版本中，我們可以得到

所以如果δ（X）是給定一個可觀測量向量X的未觀測參數θ的估計量;如果T（X）是θ的充分統計量;那么可以通過計算獲得改進的估計量，即具有較小的預期損失L的意義

，相對於θ的期望值δ在所有可能的觀察值向量X上都可以與觀察到的相同的T（X）值相匹配。

這個結果被稱為Rao-Blackwell定理。