基本介紹
- 中文名:
- 外文名:
- 提出者:
- 提出時間:




















- 伸縮變換運算元具有在整個空間進行搜尋的能力,使其滿足全局性;
- 旋轉變換運算元中,當旋轉因子充分小時,當前的最好解將變成一個局部最優解,即;

- 更新策略可以保證狀態轉移算法的收斂性,因為



- 採樣機制(它有效地避免了窮舉)和各種狀態轉變運算元的交替使用可以很好的節省搜尋時間;
- 狀態轉移中對變換因子的調整可以控制搜尋空間的幾何形態。
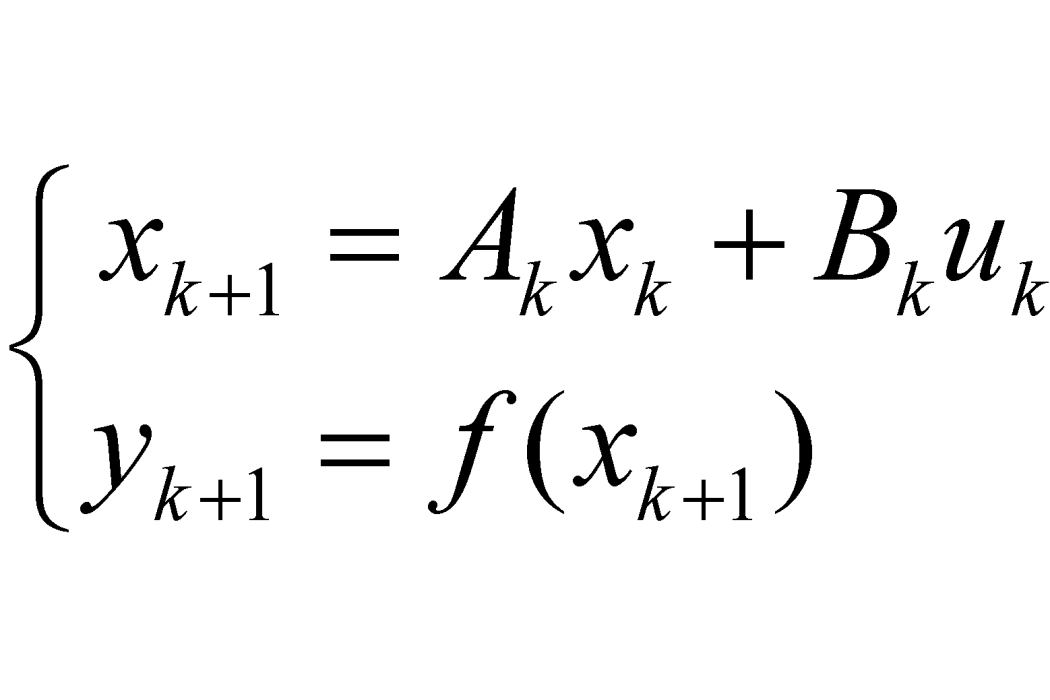
























狀態轉移算法(State transition algorithm, STA) 是由周曉君博士等於2012年提出的一種新型的隨機性全局最佳化方法,它設計的初衷是力求在儘可能短的時間內找到最最佳化問題的全局最優解或近似最優解。...
動態規劃實質上是一種以空間換時間的技術,它在實現的過程中,不得不存儲產生過程中的各種狀態,所以它的空間複雜度要大於其它的算法。如何設計動態轉移方程 如果滿足上述條件,一般可以按照以下步驟進行設計:一、確定問題的決策對象 二、...
Floyd算法狀態轉移方程 其狀態轉移方程如下: map[i,j]:=min{map[i,k]+map[k,j],map[i,j]}; map[i,j]表示i到j的最短距離,K是窮舉i,j的斷點,map[n,n]初值應該為0,或者按照題目意思來做。
狀態轉移算法是一種基於結構主義學習的新型智慧型最佳化算法,它抓住最佳化算法的本質、目的和要求,以全局性、快速性、收斂性、可控性等五大核心結構要素為指導思想進行算法設計與理論證明。它的基本思想是將最佳化問題的一個解看成一個狀態,將解...
GAF算法需要解決:等價節點的確定、狀態轉移、與現有路由協定結合等關鍵技術問題。1、等價節點的確定 這裡所謂兩個節點等價是指:對中繼轉發而言,一個節點可以代替另一個節點中繼轉發。根據這個定義,節點的等價性與通信的源節點和目的節點...
對一個確定有限狀態自動機,下述判定問題都可以判定,並且存在有效的算法。該自動機識別的語言是否為空集。該自動機識別的語言是否為有限集。該自動機是否與另一個確定有限狀態自動機識別同一個的語言。例如:有限狀態自動機:輸入串為3...
用一條沒有起點的邊指向起始狀態。除了在表述上方便以外,在研究某些問題(如“給定的DFA的語言是否為無窮集合”)時,狀態圖也提供了有效的解法。利弊 DFA是一種實際的計算模型,因為有平凡的線性時間、恆定空間的線上算法模擬在輸入流...
動態規劃狀態(state of dynamic programming)是指在多階段決策過程中,為建立模型及便於計算,引入每個階段的狀態變數。它和問題的約束條件緊密關聯。動態規劃引入適當的狀態變數,可使狀態轉移滿足無後效性的要求。如果狀態變數不恰當,將...
馬爾可夫算法是使用類似形式文法的規則在符號串上操作的字元串重寫系統。簡介 馬爾可夫算法是使用類似形式文法的規則在符號串上操作的字元串重寫系統。馬爾可夫算法被證明是圖靈完全的,這意味著它們適合作為一般的計算模型,並可以用它的簡單...
動態算法所遵循的原則是最優性原理,它可描述如下:一個最優決策序列具有下述性質:無論初始狀態和第一步決策是什麼,餘下的決策必須按照前一次決策所產生的新狀態構成一個最優決策序列。也就是說,不論前面的狀態和策略如何,後面的最...
隱馬爾可夫鏈、馬爾可夫狀態轉換模型及在量化投資中的套用內容簡介 編輯 語音 本書屬於數理金融(量化投資)的範疇, 論述了隱馬爾可夫鏈和馬爾可夫狀態轉換模型的數學原理、數值算法及在量化投資中的套用。出於完備性的考慮, 本書的前兩章...
ATN也稱為代標記的遞歸轉移網路,因為它把當前信息、如詞語、句子成分等信息存放在暫存器中,通過測試的方法來查找下一狀態,在測試通過之後執行相關的動作,然後跳到下一狀態。在做了這些擴充之後ATN算法的靈活性比較好,但是在一定程度上...
這個算法將幫助我們訓練HMM的轉移機率A和發射機率B。內容簡介 EM算法可用於含有隱變數的統計模型的參數最大似然估計,其基本思想是:初始時隨機地給模型的參數賦值(該賦值必須遵守模型對參數的限制,如從一狀態出發的所有機率的總和是1),...
(4)尋找邊界條件:給出的狀態轉移方程是一個遞推式,需要一個遞推的終止條件或邊界條件。算法實現 動態規劃的主要難點在於理論上的設計,也就是上面4個步驟的確定,一旦設計完成,實現部分就會非常簡單。使用動態規劃求解問題,最重要的...
動態規劃算法的關鍵在於解決冗餘,這是動態規划算法的根本目的。動態規劃實質上是一種以空間換時間的技術,它在實現的過程中,不得不存儲產生過程中的各種狀態,所以它的空間複雜度要大於其他的算法。選擇動態規划算法是因為動態規划算法在...
在蟻群算法的基礎上蟻群系統主要做了三方面的改進:(1) 以偽隨機比例規則進行狀態轉移。這使關於問題的先驗知識得到了更好利用,也為新路徑的選擇提供了更合理的方法。蟻群系統中引入了參數 ,可以對螞蟻探索新路徑的程度進行調節,有效...
算法描述 圖1-1給出了PAMAS協定的狀態轉移圖。從圖中可以看出,一個節點可能處於以下6個狀態中的任何一個:Idle、Await CTS、BEB(Binary Exponential Bakeoff)、Await Packet、Receive Packet以及Transmit Packet。在這個狀態圖中,狀態選擇...
2. 針對已知的模型,尋找最可能的能產生某一特定輸出序列的隱含狀態的序列:可以使用 Viterbi Algorithm 解決.3. 針對某輸出序列,尋找最可能的狀態轉移以及輸出機率:通常使用最大可能性法則 (Maximum Likelihood) 的演算法,像是 Baum-...
卡爾曼濾波(Kalman filtering)是一種利用線性系統狀態方程,通過系統輸入輸出觀測數據,對系統狀態進行最優估計的算法。由於觀測數據中包括系統中的噪聲和干擾的影響,所以最優估計也可看作是濾波過程。數據濾波是去除噪聲還原真實數據的一...
一個狀態到另一個狀態的轉移不一定是確定的。隨機化算法在內的一些算法,包含了一些隨機輸入。形式化算法的概念部分源自嘗試解決希爾伯特提出的判定問題,並在其後嘗試定義有效可計算性或者有效方法中成形。這些嘗試包括庫爾特·哥德爾、雅克...
*1 評估問題: 直接計算法(概念上可行,計算上不科學)、前向算法、後向算法 *2 解碼問題: Viterbi算法:使用動態規劃求解機率最大(最優)路徑。 近似算法:選擇每一時刻最有可能出現的狀態,從而得到一個狀態序列。*3 學...
在採用MCMC方法時馬爾科夫鏈轉移核的構造至關重要,不同的轉移核構造方法將產生不同的MCMC方法,常用的MCMC方法主要有兩種Gibbs抽樣和Metropo-Lis-Hastings算法。MCMC已經被廣泛地套用於統計分析圖像處理、信號處理、金融分析等領域。常見算法...
以蒙特卡羅方法和時序差分學習(temporal-difference learning)為代表的MDP算法屬於“無模型的強化學習(model-free reinforcement learning)”,適用於MDP的環境動力項未知的情形。在MDP的轉移機率未知時,狀態值函式 無法參與最佳化,因此隨機...
給定狀態 ,觀測矢量 的機率密度依賴於所有層的當前狀態,該機率可以用下面一個高斯機率函式來模擬 其中, 是給定狀態 第 層的均值,C 為協方差。FHMM 模型的參數可以使用期望值最大(EM)算法來估計。套用 FHMM是一種動態模式...
