基本介紹
- 中文名:牛頓-萊布尼茨公式
- 外文名:Newton-Leibniz formula
- 分類:數學
- 又名:微積分基本定理
- 時間:1677年
- 提出 :牛頓 萊布尼茨
定理定義
定義




弱化條件






公式推導
推導一




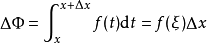








推導二





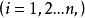








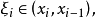


定理推廣
二重積分形式





曲線積分形式


 與格林公式和高斯公式的聯繫
與格林公式和高斯公式的聯繫




發展簡史


牛頓-萊布尼茲公式一般指本詞條














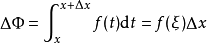













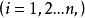








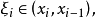









 與格林公式和高斯公式的聯繫
與格林公式和高斯公式的聯繫





牛頓-萊布尼茲公式(Newton-Leibniz formula),通常也被稱為微積分基本定理,揭示了定積分與被積函式的原函式或者不定積分之間的聯繫。牛頓-萊布尼茨公式的內容是一個...
由於名稱相似,不少人將牛頓-萊布尼茨公式與萊布尼茨公式相混淆,事實上他們是兩個完全不同的公式。牛頓-萊布尼茨公式是微積分學中的一個重要公式,它把不定積分與定...
萊布尼茲公式,也稱為乘積法則,是數學中關於兩個函式的積的導數的一個計算法則。不同於牛頓-萊布尼茨公式,萊布尼茨公式用於對兩個函式的乘積求取其高階導數。萊布尼茨...
因此,他所創設的微積分符號遠遠優於牛頓的符號,這對微積分的發展有極大影響。1714至1716年間,萊布尼茨在去世前,起草了《微積分的歷史和起源》一文(本文直到1846...
萊布尼茨於1675—1676年給出了微積分基本定理(後來又稱為牛頓-萊布尼茨公式) (A為曲線f下的圖形的面積,圖3.) 於1693年給出了這個定理的證明.以前,微分和積分作...
萊布尼茨公式給出了含參變數常義積分在積分符號下的求導法則。萊布尼茨是德國自然...在數學上,與牛頓並稱為微積分的創始人,改進了帕斯卡的加法器,設計並製造了一...
泰勒公式,套用於數學、物理領域,是一個用函式在某點的信息描述其附近取值的公式...1712年當選為英國皇家學會會員,同年進入促裁牛頓和萊布尼茲發明微積分優先權爭論...
數學公式是人們在研究自然界物與物之間時發現的一些聯繫,並通過一定的方式表達出來的一種表達方法。是表征自然界不同事物之數量之間的或等或不等的聯繫,它確切的...
在數學上,牛頓與戈特弗里德·威廉·萊布尼茨分享了發展出微積分學的榮譽。他也證明了廣義二項式定理,提出了“牛頓法”以趨近函式的零點,並為冪級數的研究做出了貢獻...
《如果牛頓沒有遇見萊布尼茲》是莫忻荏創作的網路小說,發表於晉江文學網。...... 《如果牛頓沒有遇見萊布尼茲》是莫忻荏創作的網路小說,發表於晉江文學網。 ...
積分之間的關係:若定積分存在,則它是一個具體的數值(曲邊梯形的面積),而不定積分是一個函式表達式,它們僅僅在數學上有一個計算關係(牛頓-萊布尼茨公式),其它一...
是高斯公式,斯托克斯公式的概括和總結,是單變數微積分中牛頓-萊布尼茲公式在多變數中的推廣。微分形式斯托克斯定理 編輯 利用外微分和積分運算, 我們可以得到著名的...
積分變限函式是一類重要的函式,它最著名的套用是在牛頓一萊布尼茲公式的證明中.事實上,積分變限函式是產生新函式的重要工具,尤其是它能表示非初等函式,同時能將...
積分的定義迥然不同,定積分是求圖形的面積,即是求微元元素的累加和,而不定積分則是求其原函式,而牛頓和萊布尼茨則使兩者產生了緊密的聯繫(詳見牛頓-萊布尼茨公式...
定理的第二部分,稱為微積分第二基本定理或“牛頓-萊布尼茨公式”,表明定積分可以用無窮多個原函式的任意一個來計算。這一部分有很多實際套用,這是因為它大大簡化...
牛頓萊布尼茲公式 上,積分作用不僅如此,它被大量套用於求和,通俗的說是求曲邊多邊形的面積,這巧妙的求解方法是積分特殊的性質決定的。 一個函式的不定積分(亦稱原...
